Inscription / Connexion Nouveau Sujet
Intégration !
Bonjour voici un exercice de mon DM mais je ne comprends strictement rien à l'intégration :
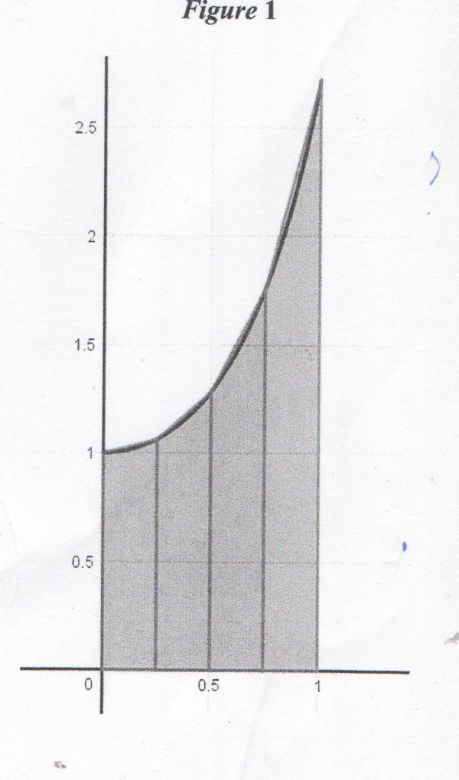
f est la fonction définie sur [0 ; 1] par f(x)=ex².
Le but de cet exercice est de chercher une approximation de l'aire du domaine I délimitée par le courbe Cf, l'axe des abscisses et les droites d'équations x = 0 et x = 1.
Partie A: méthode des rectangles
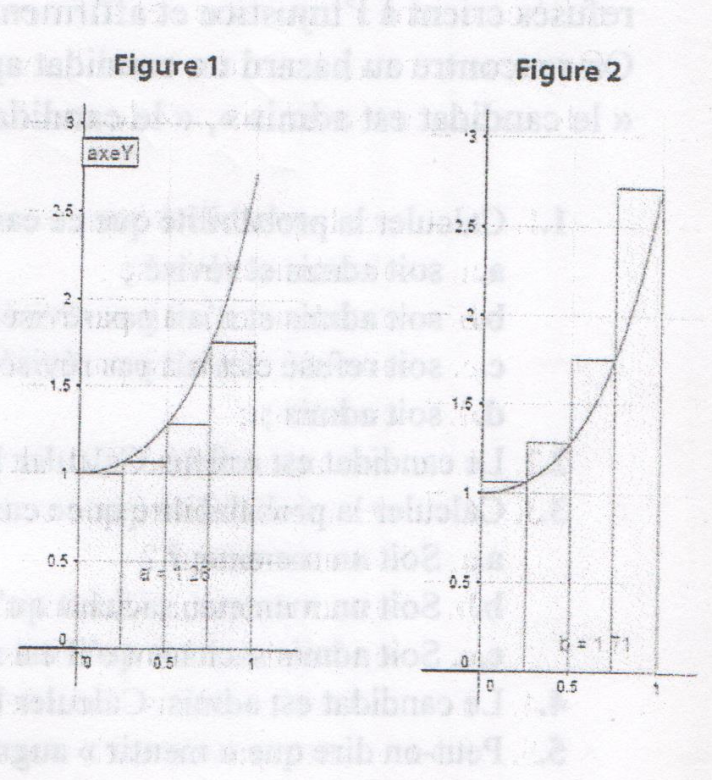
On a représenté f sur l'intervalle [0 ; 1] et des rectangles sur les deux figures ci-contre et fait afficher la somme de leurs aires a et b.
1.Déduire des deux figures ci-dessus un encadrement de I.
2.a. Quelles sont les hauteurs de chaque rectangle sur la figure 1?
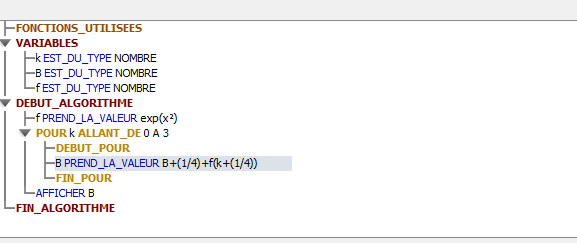
b. On considère l'algorithme suivant qui donne l'affichage de l'aire a. Explique la ligne L3 de l'algorithme.
c. Modifier l'algorithme pour qu'il affiche l'aire b.
3. Comment faire pour avoir un encadrement plus précis l'intégrale I cherchée?
En programment des algorithmes sur votre calculatrice ou sur un logiciel, déterminer un encadrement de I d'amplitude 0.01.
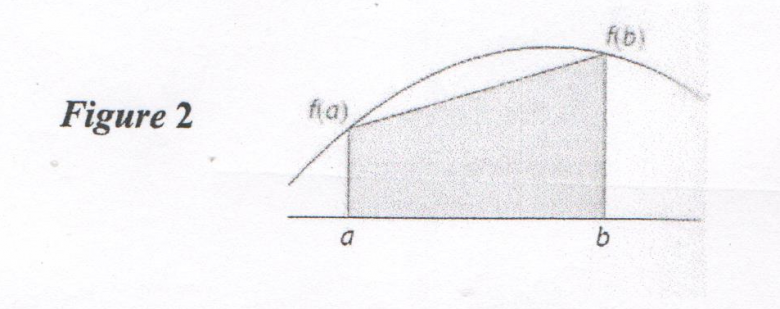
Partie B: Méthode des trapèzes
On a représenté f sur l'intervalle [0 ; 1] et des trapèzes sur la figure 1 ci-contre.
1. Préliminaires
Montrer l'aire du trapèzes obtenu en remplacement sur [a ; b]. La courbe C par un segment de droite est égale à :
(b-a)
2.Ecrire un algorithme pour l'estimation de I par la méthode des trapèzes en partageant l'intervalle [0 ; 1] en quatre partie égale.
Conclusion :
Quelle est la méthode la plus rapide pour avoir une estimation de I ?
Argumenter.
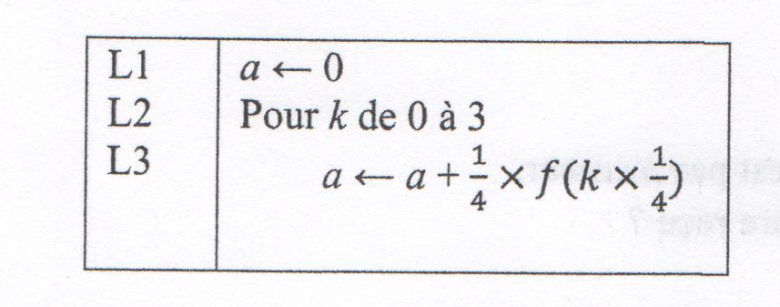
salut
ne pas comprendre est une chose ... ne pas faire d'effort pour (tenter de) s'approprier le savoir en est une autre ...
sais-tu ce que signifie
quelle est l'interprétation géométrique d'une intégrale ?
Euh non je ne comprends pas du tout je sais que permet de calculer une chose mais je ne sais pas de quoi.
Mais ici l'encadrement des deux figures c'est [0;1]
Bonjour
carpediem pourrais tu comprendre que certaines personnes en sont au début de l'apprentissage de la notion d'intégration.
Visiblement coatch en est au tout début et n'a jamais vu le signe  .
.
Fin de l'aparté avec carpediem
Dans toutes ces multiples questions qu'as tu essayé ? Pourquoi n'arrives tu pas à avancer ? Tu ne connais pas quoi dans les questions posées ?
Bonjour cocolaricotte,
Pour la 1. l'intervalle des deux figures est [0;1]
Mais pour la 2.a. je ne trouve pas
Je continuerai demain. A demain.
Bonne soirée.
Il faut nous en dire plus sur ce que tu as fait et trouvè et sur ce que as cherché et pas trouvè.
On ne va pas faire l'exercice à ta place.
cocolaricotte : effectivement il n'est pas besoin de calcul intégral ...
cependant s'il ne sait pas calculer l'aire d'un rectangle (de quatre), de faire la somme de comparer des aires (il semble évident que si un disque est inclus dans un carré alors son aire est inférieure à celle du carré ...
quant à l'algorithme franchement il n'y a pas plus élémentaire ...
j'accepte donc tout à fait ta remarque : je me suis un peu précipité ... mais bon faut pas abuser tout de même sur le niveau de difficulté élémentaire de cette exo ...
Il faut donc accepter que les personnes qui postent, ici ont des difficultés, sinon ils ne posteraient pas.
Aider ceux qui savent faire je ne vois pas l'intérêt !
coatch
Cela ressemble à un autre exercice où tu as reçu de l'aide !
Il faudrait peut être commencer à te prendre en charge toi , tout seul , sans nous.
bonjour à tous les deux,
je n'ai jamais demandé à ce que l'exercice soit fait par les correcteurs , ce n'est pas le but .
Sinon , à quoi cela servirait. Recopier un exercice sans comprendre ce n'est pas mon but.
C'est sûr qu'il y a des choses plus dures que d'autres à comprendre en mathématiques. Avec un cours , c'est clair que ce serait plus simple pour pouvoir faire cet exercice.
Mais voilà, les exercices sont donnés avant même de voir les cours. Chaque personne , chaque professeur a sa méthode .
Quand je poste un exercice, si je sais le faire je mets mes réponses je peux vous le certifier .
Après peut être pour toi Carpediem , l'algorithme est facile . Pour d'autres, c'est un peu plus compliqué.
Je vais essayer de le faire cet exercice avec mes propres connaissances et je mettrai mes réponses .
J'espère que quelqu'un pourra me dire si c'est correct ou pas .
Merci pour votre compréhension à tous .
Pour la hauteur des rectangles,
le 1er rectangle : e0²=1
le 2nd rectangle : e(1* 1.06
1.06
le 3eme rectangle : e(2* 1.28
1.28
le 4eme rectangle : e(3* 1.76
1.76
Merci
Pour la 2.b.
La ligne 3, je pense:
a correspond à l'aire ; le "+1/4" qui suit le a je pense qu'il permet de passer à la suite des autres rectangles ; le f correspond à la fonction f(x) = ex² ; par contre le k est une constante qui permet de calculer une hauteur d'un rectangle choisi ?
Merci
Je n'ai pas vérifié tes calculs pour f(0) , f(1/4) , f(2/4)=f(1/2) , f(3/4)
a est bien la variable qui cumule les aires des différents rectangles
k compte le nombre de rectangles dont on additionne les aires du "0ème" celui qui correspond à celui dont la hauteur est f(0) , au dernier celui qui correspond à celui dont la hauteur est f(3/4).

S'il vous plait quelqu'un peut me dire si j'ai bon 
D'accord mais j'essaye de le faire avec algobox mais celui ci ne fonctionne pas 
Un peu de patience ! On ne passe pas notre vie sur le forum ! On a d'autres activités !
Les personnes qui te répondent sont des bénévoles qui acceptent de donner un peu de leur temps libre pour aider gratuitement ceux qui ont besoin d'un coup de main.
Si tu saisis ces 3 lignes et rien que ces 3 lignes, sur Algobox normal qu'il ne donne rien.
La fonction f est elle définie ?
Cet algo ne fait rien afficher !
bonjour coatch
question1)
sauf erreur de ma part, je n'ai pas vu de bonne réponse de ta part à cette question.
regarde les 2 figures, d'aires respectives a et b
à ton avis, quel encadrement peux-tu en déduire de l'aire sous la courbe de f ?
-----
ton algo ci-dessus (13h08) ne peut pas marcher :
on le déroule à la main pour que tu comprennes pourquoi
- tu définis les 3 variables k, B, et f ---- la machine reconnaitras ces variables-là
- "f prend la valeur ex²"
==> la machine ne connait pas la variable x
et x vaut combien ? comment veux-tu qu'elle puisse calculer "e puissance" un nombre inconnu ?
ni toi ni moi ne pouvons le faire : la machine encore moins.
il faut bien que tu comprennes que si la machine est capable de calculer des milliers de fois plus vite que le commun des mortels, elle n'est capable d'aucune imagination : tu dois tout lui détailler si tu veux en tirer un résultat.
on oublie ton algo pour le moment
---
hauteur des rectangles figure 1
c'est bon
mais inutile de calculer des valeurs approchées pour le moment, garde les valeurs exactes, mais élégament simplifiées 
par ex
f(1/4) = e(1/4)² = e1/16
etc
---
je te propose de commencer par calculer à la main, sur le brouillon, l'aire des 2 premiers rect.
c'est le mm principe que l'exo d'il y a qq semaines.
note les détail de tes calculs
---
ensuite seulement, prends l'algo de l'énoncé
puis déroule-le à la main (comme je t'ai toujours conseillé...)
L1 : a=0 ------ au départ, l'aire est initialisée à 0
L2 : pour k allant de 0 à 3 ------ une boucle qui commence avec k=0
L3 : a = a + 1/4 * f(k * 1/4)
k * 1/4 = ...? tu calcules et tu l'écris
f( k * 1/4) = ...?
1/4 * f(k * 1/4) = ...? ==> ça ne te rappelle rien ce calcul ?
a + 1/4 * f(k * 1/4) = ...?
a = a + 1/4 * f(k * 1/4) ------- fin du 1er tour de boucle 'pour"
puis on passe au k suivant ---> donc k = 1
et on recommence les instructions dans la boucle..
à la fin de ce second tour de boucle, que représente la valeur contenue dans "a" ?
je dois filer; j'essaie de passer te lire + tard
allez courage
le début de cet exo n'est pas très différent de ce que tu as déjà fait
Euh pour l'aire des rectangles, j'étais partie pour utiliser le formule :
1er triangle : 1/4 * e0*1/4? Est ce que c'est ça ?
"l'encadrement des figures ce n'est pas [0;1] " --- ce n'est pas la question posée
"1er rectangle : 1/4 * e0*1/4? " ---  regarde ce que tu as écrit à 12h31
regarde ce que tu as écrit à 12h31
allez, on se concentre
je repasserai quand tu auras bien avancé.
a+
question 2
aire du premier rectangle : f(0*1/4)
aire du deuxième rectangle f(1*1/4)
aire du troisième rectangle f(2*1/4)
aire du quatrième rectangle f(3*1/4)
1) non
tu as déjà donné cette réponse plusieurs fois... tu comptes m'avoir à l'usure ? 
et puis tu peux vérifier que cette réponse est incohérente ! surtout si on te dit plusieurs fois que ce n'est pas la bonne réponse.
I, c'est l'aire sous la courbe (délimitée par les droites données dans l'énoncé, je n'y reviens pas)
il suffit de regarder la figure 1 pour voir que cette aire est plus grande que l'aire du carré de coté 1
(1 en abscisse et 1 en ordonnée)
donc, même très "à la louche", forcément I ne peut pas être compris entre 0 et 1.
2) là c'est du n'importe quoi.
tu as calculé f(0*1/4) pour voir? et comparé avec l'aire du 1er rectangle sur la figure ?
ça contredit ce que tu as écrit hier 03-02-18 à 12:31
et que j'ai confirmé à 14:54
l'aire d'un rectangle... quand même, coatch ...
j'ai comme l'impression que tu lis les messages en oblique, les écouteurs MP3 sur les oreilles,
et que tu réponds le 1er truc qui te vient, en tout cas que tu n'es "pas dedans".
je me trompe ?
je (on) passe du temps à rédiger, à réfléchir que te dire pour t'aider.
peut-être que je m'y prends mal, mais tes réponses jetées aux fléchettes... non
je me permets de te dire tout ça parce que tu sais que je t'aide volontiers sur les topics.
toutefois, si tu ne fais pas d'effort pour :
- lire très attentivement ce que j'écris : l'écriture est le seul lien possible via internet (donc on s'isole , on se concentre)
- réfléchir, relire l'énoncé, te relire, comparer la cohérence des données et tes résultats
- garder à l'esprit qu'au bac personne ne te tiendra la main entre chaque réponse
alors, je suis désolée, mais, pour ma part, je ne saurai pas faire. :/
à toi d'écrire la suite de l'histoire, ou pas 
bien amicalement
2.a
Pour la figure 1, les hauteurs des rectangles sont :
f(0) = e0² = 1
f(1) = e(1 
)
 1.06
1.06
f(2) = e(2
)
 1.28
1.28
f(3) = e(3
)
 1.76
1.76
2.b.
L3 " a<-a+ f(k
f(k
)
Le f(k
) permet de calculer la hauteur et
permet de passer de rectangles en rectangles soit la largeur et le a correspond à la variable qui cumule les aires des différents rectangles.
Donc la L3, permet de calculer l'aire des différents rectangle.
la 2.c.
Avant pour a, on avait :
a<-0
Pour k de 0 à 3
a<-a+
 f(k
f(k 
)
Donc en toute logique,
b<-0
Pour k de 0 à 3
b<-b+
 f(k
f(k 
)
Mais pour "Pour k de 0 à 3" je me demande si c'est pas plutôt "Pour k de 1 à 3" puisque que l'on est au dessus de la courbe ?
Après le calcul je pense qu'il y a des "+1" qui se rajoutent ....
Bonjour Carita
Non je te promets que je ne réponds pas comme ça sans réfléchir, je n'ai pas d'écouteurs aux oreilles, j'essaie de me débrouiller par moi même avec des cours que je prends sur internet car je n'ai aucun cours pour m'aider et des réponses que tu me donnes . Je n'ai que des brouillons devant moi et rien d'autres.
Désolée , si tu pensais cela mais franchement non . J'aimerais pouvoir comprendre dès que quelque chose est marqué .
J'espère que tu ne m'en veux pas et que tu veux continuer à m'aider STP
Merci 
Là j'ai remis des réponses que j'avais trouvé sur mes brouillons
3.
a 
 b
b
Si l'on veut un encadrement plus précis, il faut que les rectangles sur les figures soient de moins en moins large donc tendent vers l'infini et par ce fait d'être plus proche de l'aire de la courbe.
Est ce que je peux mettre :
13:36
plus simple que ça :
d'après les figures 1 et 2, on voit que l'aire I est comprise entre l'aire a et l'aire b.
donc a < I < b --- voilà la réponse attendue : à ce niveau de l'exo, on n'a pas encore demandé de calculer a et b
(c'est bien l'intégrale que tu écris, mais l'énoncé ne cite pas expressément cette notion)
ps : juste par curiosité, comment as-tu trouvé ces valeurs : a = 1.23; b=1.71 ?
13:49
2.a) f(x) = ex²
en tenant compte de mon message de 03-02-18 à 14:54,
f(0*1/4) = e0² = 1
f(1*1/4) = e()² = e1/16
f(2*1/4) = f(1/2) = e()²= e^?
f(3*1/4) = ...?
ce sont en effet les hauteurs des rectangles
2.b.
L3 " a<- a + * f(k

)
Le f(k
) permet de calculer la hauteur ---- (d'un rectangle), oui
permet de passer de rectangles en rectangles --- non, ce 1/4 représente la largeur du rectangle
donc la multiplication de la hauteur f(k
) par la largeur (1/4) permet de calculer l'aire du rectangle en cours
==> on a découpé l'unité des abscisses en 4, pour base de chaque rectangle
donc la largeur de chaque rectangle est de 1/4
tu es bien d'accord avec ça?
a correspond à la variable qui cumule les aires des différents rectangles. ---- oui
Donc la L3, permet de calculer l'aire des différents rectangles.... et de les cumuler
a est la somme des aires des rectangles de la figure 1
donc L3 calcule a, et (devrait) affiche(r) a.
ps : il ne t'a pas échappé que l'algo fourni est incomplet : que manque-t-il à ton avis?
juste par curiosité, comment as-tu trouvé ces valeurs : a = 1.23; b=1.71 ?
C'est écrit dans les figures
 je ne l'avais même pas vu.
je ne l'avais même pas vu.Ah je viens de comprendre pourquoi tu as mis
f(2*1/4) = f(1/2) =f(2*1/4) = f(1/2) = e()²= e^= e^?
f(3*1/4) = ...?
Donc
f(2) = e2* = e(
)²= e1/4
f(3) = e3* = e(
)²= e9/16
14:21
je sais bien que tu es une élève sérieuse (sinon je ne reviendrai pas  )
)
mais parfois tes réponses sont bien déconcertantes...
je ne te demande pas pourquoi tu n'as pas de cours, ça ne doit pas être facile,
mais sur internet, il y a souvent des erreurs dans les cours... mm moi, j'en vois !
il serait préférable de travailler avec 1 ou 2 livres de cours, et de te faire de petites fiches récapitulatives.
fin de l'intermède, on reste concentrées 
---
14:07
2.c.
b<-0
Pour k de 0 à 3
b<-b+
 f(k
f(k 
)
Mais pour "Pour k de 0 à 3" je me demande si c'est pas plutôt "Pour k de 1 à 3" puisque que l'on est au dessus de la courbe ? --- bravo, bonne question ! mais de 1 à 3, ça fait 3 rectangles, et non pas 4 comme souhaité.
en effet, si tu gardes tel quel (de 0 à 3) , les hauteurs prises seront les mêmes que pour "a"
i.e. f(0), f(1/4), f(1/2) et f(3/4)
et donc... tu vas recalculer a, et non pas b !
le fait de changer de nom de variable n'a aucune incidence pour la machine
en fait, pour b, les hauteurs sont : f(1/4), f(1/2), f(3/4) et f(1)
donc, tu peux faire de 2 façons différentes :
soit
b<-0
Pour k de 0 à 3
b<-b+
 f((k+1)
f((k+1) 
)
==> de 0 à 3, on aura bien 4 itérations dans la boucle
pour k=0
k+1=1
f((k+1) 
)= f(1/4)
on a ainsi bien la hauteur du 1er rectangle
pour k=1,
k+1=2
...etc.
comprends-tu bien le pourquoi du "k+1" ?
soit
b<-0
Pour k de 1 à ...?
b<-b+
 f(k)
f(k) 
)
Pour l'algorithme :
que manque-t-il à ton avis?
Il manque l'affichage de a et mettre fin à la boucle ...
Oui oui le k + 1 j'avais compris et je l'avais écrit sur ma feuille mais je n'étais pas sûre.
Et b<-0
Pour k de 1 à n+1 -> en fait je veux indiquer le rang supérieur mais je ne sais pas quoi mettre 
b<-b+
 f(k)
f(k) 
)
14:27
3.
a 
 b
b
mets de coté cette notation, elle n'est pas utile dans cet exo
c'est un exercice d'approche de la notion d'intégrale
tu n'es pas censée en savoir plus sur son écriture.
et de toutes façons, ce n'est pas l'objet de la question posée.
---
Si l'on veut un encadrement plus précis, il faut que les rectangles sur les figures soient de moins en moins larges et par ce fait d'être plus proche de l'aire de la courbe. ---- exactement !
donc tendent vers l'infini --- pas très clair...
je suppose que tu as voulu dire que c'est le nombre de rectangles qui doit tendre vers l'infini, et non pas les rect. eux-mêmes;
le début de l'exo propose un découpage en 4
si on augmente ce nombre (5, 6, 10, 100....et plus), le découpage sera plus fin, et on se rapprochera de l'aire réelle I.
----
Est ce que je peux mettre :
non
écrit comme ça c'est faux : ce n'est pas x qui doit tendre vers 0
mais le nombre n de rectangles qui tend vers l'infini.
comme déjà dit, laisse tomber ces écritures pour le moment.
pour 1.23 et1.71 sur les graphiques
mdr !
je n'avais pas vu non plus (dis celle qui demande de tout bien lire...) 
je continue
14:43
f(3) = e(3²)
 1.76
1.76
là je vais faire celle qui a fait exprès de ne pas voir...
14:55
f(2) = e(2*)² = e(
)²= e1/4
f(3) = e(3*)² = e(
)²= e9/16
juste
mais tu avais oublié de saisir les "carrés" sur les expressions mises en rouge
15:00
Pour l'algorithme : Il manque l'affichage de a et mettre fin à la boucle
PARFAIT !
faudra donc penser à le rajouter à la question 2c)
15:08
Et b<-0
Pour k de 1 à 4
-> en fait je veux indiquer le rang supérieur mais je ne sais pas quoi mettre 
ce qu'il faut savoir pour les boucles :
dans une boucle, en l'absence de précision contraire, le pas est automatiquement égal à 1
donc quand on écrit :
pour k allant de 1 à 4
...
fin pour
k va prendre successivement les valeurs 1 puis 2 puis 3 puis 4
sans qu'on lui demande d'ajouter 1 à k.
l'incrémentation de 1 en 1 est automatique : on n'a pas à s'en occuper (chouette! enfin, la plupart du temps...)
ça répond à ta question ?
Oui en plus j'allais poser : est ce que c'est bon ? 
b<-0
Pour k de 1 à 4
b<-b+1/4 * f((k+1) * 1/4)
fin pour
Afficher b
si j'ai bien suivi, on en est à la question 3 : ça va se corser un peu...
En programmant des algorithmes sur votre calculatrice ou sur un logiciel, déterminer un encadrement de I d'amplitude 0.01.
DES algos...
je te conseille de commencer par programmer sur algobox celui de l'énoncé dûment complété et adapté.
à part que tu aies déjà avancé sur cette question ?
ps : sinon, tu peux commencer la partie B
je reviens te lire + tard.
15h27
parfait 
a+
oups j'ai lu trop vite... il y a une erreur
b<-0
Pour k de 1 à 4
b<-b+1/4 * f((k+1) * 1/4)
fin pour
Afficher b
déroule- le à la main (conseillé) ou relis 15:00