Inscription / Connexion Nouveau Sujet
Isométries et nombres complexes.
Bonjour ,
Merci d'avance. 
A et B sont deux points du plan orienté tel que AB=6 cm.
On note r1 la rotation de centre A et d'angle
la rotation .
r2 la rotation de centre B et d'angle .
Pour tout point M du plan, on note M1 et M2 les images respectives de M par r1 et r2.
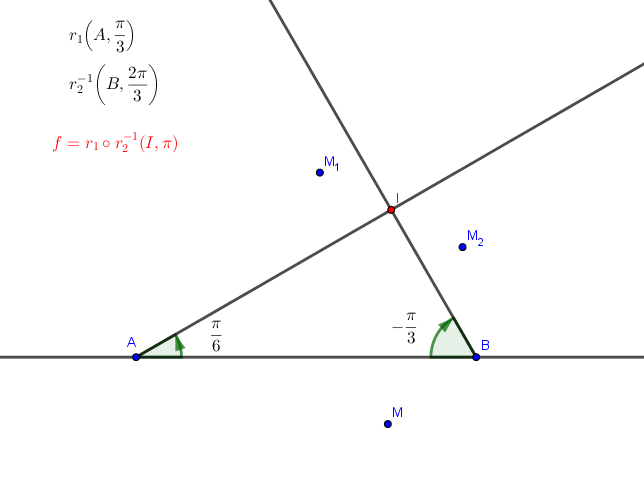
1) Placer un point M sur la figure et construire M1 et M2.
2) Le but de cette question est de démontrer que, pour tout point M du plan le milieu du segment [M1M2] est un point fixe I.
On pose .
a) Déterminer f(M2).
b) Montrer que f est une symetrie centrale.
c) En déduire que le milieu du segment [M1M2] est un point fixe I que l'on précisera dur la figure.
3. Dans cette question, le plan est muni d'un repère orthonormé direct tel que A
et B aient pour affixes respectives -3 et 3.
On note z1 et z2 les affixes respectives de M1 et M2.
M est un point du plan, distinct de A et de B , d'affixe z.
a) Exprimer z1 et z2 en fonction de z.
b) Montrer que .
c) Montrer que : (k de Z) et
.
d) Déterminer l'ensemble (Γ) des points M du plan tel que M , M1 et M2 soient alignés.
Réponses
1) r1= R(A ; π/3)
r2=R(B ; -2π/3)
r1(M)=M1 <==>
r2(M)=M2 <==>
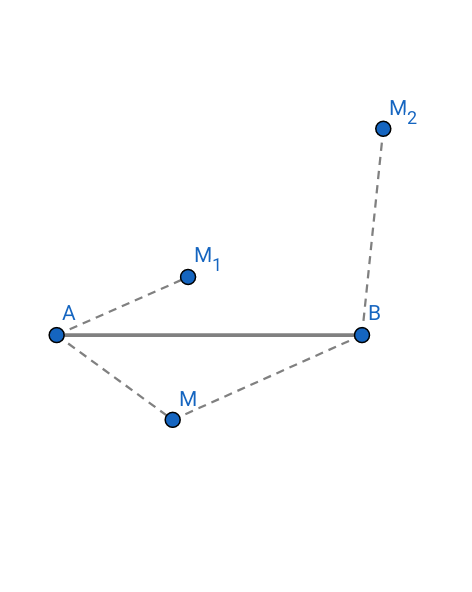
2) .
a)
b) f est la composée de deux rotations d'angles π/3 et 2π/3.
==> f est une rotation d'angle π/3+2π/3=π.
*Déterminons le centre de f.
f(M2)=M1
f(B)=B' tel que .
Le centre de f est alors le point d'intersection des médiatrices de [M1M2] et [B'B].
Or (BB') est la médiatrice de [M1M2] et (M1M2) celle de [BB'].
==> (BB') et (M1M2) se coupent au milieu de [M1M2] et [BB'].
C'est à dire [M1M2] et [BB'] ont même milieu .
==> et
.
D'où f est la rotation de centre et d'angle π.
C'est à dire la symétrie centrale de centre .
c) Le milieu du segment [M1M2] est le point .
Ce n'est pas la peine de délayer comme tu le fais :
est soit une translation soit une rotation.
Ce n'est pas une translation donc c'est une rotation. son angle vaut .
C'est donc une symétrie centrale de centre fixe.
Il me semble que nous avons déjà vu ensemble comment construire le centre d'une rotation composée de deux rotations.
Je cherche ....
Bon, ce n'était pas toi mais tu peux jeter un œil à ceci : ![]() composé de rotation
composé de rotation
Un conseil tout de même :
en 3)a), on te demande :
a) Exprimer z1 et z2 en fonction de z.
On pourrait imaginer calculer
Ce serait une erreur : la formule donnant l'expression complexe d'une rotation fait intervenir des exponentielles. Il faut les conserver telles quelles en vue de 3)b).
Les calculs se passent alors très bien.

3)c) La première ... et la seconde :
1 ) Tu passes aux arguments dans la relation précédente (avec interprétation géométrique).
2) Tu passes aux modules dans la relation précédente (avec interprétation géométrique aussi).
C'est quasiment immédiat 
Voyons:
Je te rappelles qu'en général :
1) (fais-moi grâce des "mes")
2) et que l'argument d'un produit, c'est la somme des arguments (toujours modulo )
Là, il faut que tu réfléchisses un peu.
Il faut utiliser le 1 (la relation entre angles orientés) du 3)c)
Ce n'est pas difficile 
Bien : tu as disparu.
Je ne pourrai pas intervenir demain. En attendant, ce fil mérite bien de "l'animation".
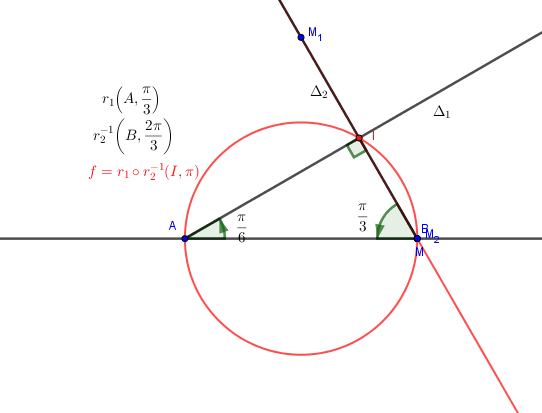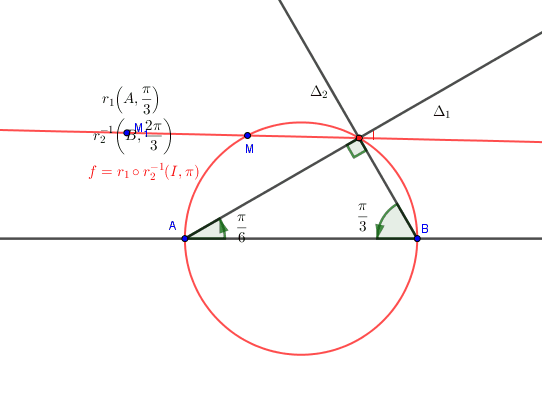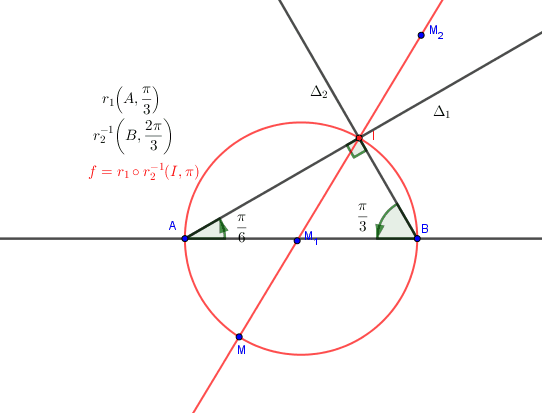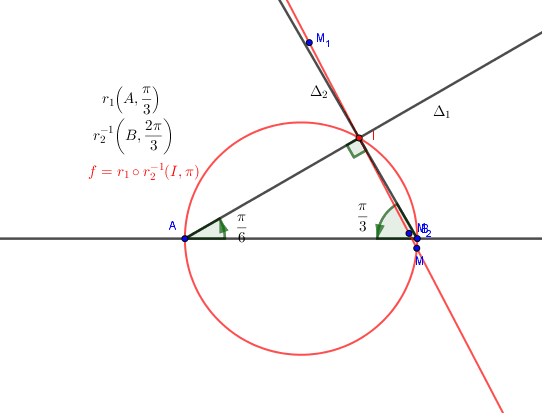
Attention aux cas ou
Bonne soirée. 
Donc il faut que
C'est à dire que Le point M appartient au cercle de diamètre [AB].
D'où (Γ) est le cercle de diamètre [AB].
Donc il faut que
Modulo
D'où (Γ) est le cercle de diamètre [AB].
Privé dans un premier temps des points
Je t'invite à regarder ce qui se passe lorsque
De rien matheux14.
A l'avenir, fais très attention à ces histoires de modulo (ici ou
).
Ce n'est pas la même chose 
Bonsoir matheux14,
J'avais laissé courir, mais j'ai des regrets :
r1(M)=M1 <==>
r2(M)=M2 <==>
Tu utilises des équivalences à tout va. Ici, elles sont fausses. Des implications, soit. Mais jamais des équivalences.
Ce genre d'abus est source d'erreurs.