Inscription / Connexion Nouveau Sujet
Le Viaduc de Garabit
Bonjour, j'ai un problème à résoudre mais je ne vois pas comment m'y prendre en voyant le sujet...
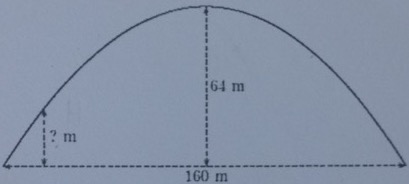
"L'arche supérieur du viaduc de Garabit a la forme d'une parabole P. Déterminer sans mesure la hauteur exacte de l'arche à 20 m du bord."
Bonjour,
avec les trois points (les deux bords et le sommet),
trouver l'équation (y = f(x)) de la parabole, dans un repère choisi pour simplifier les calculs par exemple.
et finalement calculer la valeur de ce f(x) en le point adéquat (celui à 20m du bord)
J'ai donc ttouvé mes 3 points : A(0;0) B(80;64) C(160;0). Ensuite je ne comprend pas comment trouver (y=f(x))
va pour ce repère là
pour trouver f(x), tu écris que puisque c'est une parabole,f(x) = ax² + bx + c
et il faut chercher c pour que y = ax² + bx + c soit satisfaite pour chacun de ces points
par exemple, que A (0; 0) : f(0) = 0 : c'est à dire a*0² + b*0 + c = 0
B(80; 64) : f(80) = 64 ...
C(160; 0) : f(160) = 0 ...
ça te donne un système de deux équations à deux inconnues a et b (c est immédiat)
tu peux aussi chercher f(x) sous une autre forme. par exemple la forme factorisée, ou la forme canonique, si tu as vu ça.
(calculs plus ou moins semblables, il faut de toute façon écrire que ça passe en A, B, C)
je t'en ai donné une des trois équations :
A (0; 0) : f(0) = 0 : c'est à dire a*0² + b*0 + c = 0
j'ai juste remplacé x par 0 (l'abscisse de A) et j'ai écrit que c'était égal à 0 (l'ordonnée de A)
à partir de "y = ax² + bx + c"
en plus de ça, celle ci se simplifie en c = 0 (0² ça fait 0 et a multiplié par 0 ça fait 0 quelle que soit la valeur de a etc)
tu fais pareil avec les autres
faut pas pousser, c'est du simple remplacement de valeurs numériques de x et de y dans "y = ax² + bx + c" écrit tel quel !!!
B(80; 64) : f(80) = 64 ...
tu remplaces x par 80 (l'abscisse de B) et y par 64 (l'ordonnée de B) dans cette écriture
et pareil pour C
tout ça se fait quasiment "au traitement de texte" remplacer x écrit x par 80 écrit 80 !!!
et tu peux même les simplifier dès maintenant en remplaçant c par 0 qu'on connait maintenant (lire ci dessus)
Est ce que c'est bon si je fais avec la forme canonique : pour le point B: alpha=80 et beta=64
-(x-80)^2+64
<=>-(x^2-2*x*80+80^2)+64
<=>-(x^2-160x+6400)+64
<=>-x^2+160x-6336
Donc a=-1 b=160 c=-6336
la forme canonique si tu veux mais tu en oublies un bout
ce n'est pas -(x-80)^2+64 mais -a(x-80)^2 + 64
et "a" on ne le connait pas
d'ailleurs tu vois bien que ton raisonnement est faux puisqu'il ne tient pas compte des extrémités
et tu vas retomber dans ton même blocage mental complet :
pour trouver "a" il faut écrire que la courbe passe par A (0; 0) (ou par C (160; 0) mais ce sera plus compliqué)
c'est à dire remplacer x par 0 et y par 0 dans y = -a(x-80)^2 + 64
dans le but d'obtenir une équation en l'inconnue "a" qu'il faudra résoudre...
faut pas tout mélanger
soit tu fais tout avec la forme développée y = ax² + bx + c
soit tu fais tout avec la forme canonique y = a(x- )² +
)² + 
alors maintenant tu reviens à la forme développée, pourquoi pas mais tiens toi à une seule des deux méthodes
avec la forme développée y = ax² + bx + c on a déja trouvé une première équation (je te l'ai donnée)
"passe par A (0, 0)" ====> c = 0
"passe par B (80; 64)" ===> 64=a*6400+b*80+c parfaitement. (et comme on sait que c = 0 ça se simplifie en 64 = 6400a + 80b
on garde ça au chaud.
"passe par C (160; 0)" ===> à faire pareil
pour l'instant c'est de l'écriture des équations
quand on les aura écrites on cherchera à les résoudre...
AUTRE METHODE différente
à partir de la forme canonique y = a(x- )² +
)² + 
on profite ici que les inconnues  et
et  tombent toutes cuites "sans calcul" par simple définition du sommet
tombent toutes cuites "sans calcul" par simple définition du sommet
y = a(x-80)² + 64
et il ne reste qu'une seule vraie inconnue "a"
on écrit que la courbe passe par A(0; 0) sur cette forme canonique là
pas une autre (pas sur ax²+bx+c, c'est l'autre méthode)
c'est alors très simple. fais le
je ne l'avais pas proposée dès le départ car j'ignorais si tu connaissais la forme canonique ou pas.
mais tu vois bien que avec la forme canonique les calculs seront tout de suite bien plus simples !!!
Du coup j'ai pris la forme développée et pour les 3 point j'ai :
A(0;0): f(x)=ax^2+bx+c
<=>0=0a+0b
B(80;64): <=>64=6400a+80b
C(160;0):<=>160=25600a+0b
Est-ce correcte?
A(0;0): f(x)=ax^2+bx+c
<=>0=0a+0b absurde on ne sait pas encore que c = 0 quand on écrit cette équation
c'est 0 = 0a + 0b + c
et c'est cette équation là qui donne c = 0
le reste est OK, en tenant compte de c = 0 désormais connu.
il te reste donc les deux équations pas franchement sympathiques :
64=6400a+80b
0=25600a+160b
on peut (doit) déja les simplifier !!
en divisant par 16 la première (PGCD de 64, 6400 et 80)
4 = 400a + 5b
et par 160 la seconde :
0 = 160a + b
ce qui est déja bien plus sympathique parce que de la seconde on peut extraire b "en fonction de a" sous une forme très simple (sans fractions) et remplacer dans la première etc...
Il me semble que tu as appris à résoudre au moins l'année dernière des systèmes de deux équations à deux inconnues
le résultat de la résolution d'un système d'équations c'est :
a = valeur numérique
b = valeur numérique
c = valeur numérique (= 0 ici)
pas des expressions du genre a = expression avec une autre inconnue qu'on ne connait pas (b) !!
je te disais
<< de la seconde on peut extraire b "en fonction de a" >>
b=-160a OK
<< et remplacer dans la première >>
la première c'est 4 = 400a + 5b
remplacer b par -160a ça donne :
4 = 400a + 5*(-160a)
c'est ça qu'il faut faire pour résoudre un système par substitution...
etc (la dernière équation écrite ici étant une simple équation du premier degré à une seule inconnue "a" tu dois savoir la résoudre !)
une fois que tu auras "a", tu pourras en déduire b = -160a = ...
et donc l'équation du viaduc est y = -1/100x² + 1,6x
et tu peux maintenant terminer l'exo... (calculer la hauteur à l'endroit indiqué)
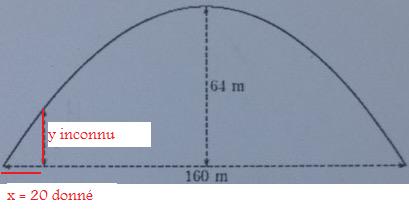
x c'est l'abscisse et y c'est l'ordonnée
tu vois bien que sur le dessin le "?" est marqué sur un segment vertical, donc une ordonnée, c'est l'ordonnée qui est inconnue ("?") et l'abscisse qui est donnée (20m avec ton repère).
En résolvant l'équation je trouve : x=0 ou x=160 donc pour moi ce n'est pas logique.
-1/100x^2+1,6x=20
<=>-1/100x^2+1,6x-20=0
<=>x(-1/100x+1,6)-20=0
<=>x=0 ou -1/100x+1,6=0
<=>x=0 ou x=160
en résolvant quelle équation, diable ???
il n'y a aucune équation à résoudre
juste remplacer x par 20 dans y = -1/100x² + 1,6x
20 c'est l'abscisse, x, et elle est donnée, c'est 20, et on cherche y, la hauteur à cette distance x = 20 du bord
toi tu cherches avec ton équation les valeurs inconnues de x pour lesquelles y serait égal à 20 !!
tu vois bien que ça n'a aucun rapport avec la question !
(et que en plus ta résolution est fausse, mais basta, vu que ce n'est pas ce qu'on demande)



