Annuler
connectez vous
probabilités en post-bac
- Un best-of d'exos de probabilités (après le bac)
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Loi de Poisson QCM
Posté par stolendance
Bonjour 
Je ne suis pas d'accord avec la correction de ce QCM, en effet la correction présente dans mon cours donne pour réponse l'item E. Sauf que d'après mes calculs l'item D est la bonne réponse.
Pour décrire l'affluence aux urgences, le directeur
d'un hôpital s'interroge sur le nombre d'adultes venant
aux urgences pendant une après-midi. En supposant que
ce nombre suit une loi de Poisson de paramètre 20, quelle
est la probabilité pour que plus de 10 adultes viennent aux
urgences une après-midi ? Dire LA proposition vraie
A. Elle est nulle
B. Elle est égale à 0,003
C. Elle est égale à 0,011
D. Elle est égale à 0,371
E. Elle est supérieure à 0,95
En effet, on est en présence d'une loi de Poisson de paramètre 
= 20 et k>10 donc d'après la table de la loi de Poisson on a :
P(X>10) = P(X=11) + P(X=12) + P(X=13) +...+ P(X=18)
= 0.011 + 0.018 + 0.027 + 0.039 + 0.052 + 0.065 + 0.076 + 0.084
= 0.372 --> Item D
Merci de me confirmer qu'il s'agit d'une erreur ou peut-être suis-je passée à côté de quelque chose ?
Merci d'avance
Bonjour,
il est plus rapide de faire le total q des valeurs inférieure ou égales à 10 puis de donner comme réponses 1-q
Ici tu oublies toutes les valeurs plus grandes que 18, et leur proba n'est pas négligeable.
Sans calcul et sans table, je dirais que la valeur est proche de 1 et très vraisemblablement supérieur à 0,99.
Donc réponse E.
Finalement j'ai fait le calcul, la proba pour qu'il y ait plus de 10 admissions est environ de 0,9891.
J'ai fait ça avec la table qui nous est fournie pour la loi de Poisson le jour du concours et elle ne va que jusqu'à 18, c'est pour ça
Merci beaucoup
Ah je n'avais pas pensé à faire comme ça merci beaucoup Razes, c'est la meilleure solution vu que je n'ai pas le droit à la calculatrice
Je trouve :
P(X>10) = 1 - P(X<= 10)
= 1 - (0.001 + 0.001+ 0.003 + 0.006)
= 0.989
donc l'item E est bon
C'est bon. Pour la valeur, j'ai calculé cela avec EXCEL et j'ai obtenu une valeur différente 0.997.
En tout cas c'est supérieure à 0,95 donc c'est l'item E.
Pour la valeur, c'est correct.
Tu peux tester avec EXCEL en tapant dans une cellule l'expression: qui correspond à
P(X> 10) = 1- (Valeur calculé par Excel) = 0.989
salut,
à partir de 20 (ou 19 ) on utilise l'approximation normale
sans approximation:
1-poisson_cdf(20,10) donne 0.989188281173
avec l'approximation par N(20,20) et en faisant une correction de continuite:
1.0-normal_cdf(20,sqrt(20),10.5) donne 0.983175987063
verification effectuee avec le logiciel de calcul formel Xcas (libre et gratuit)
Bonjour tout le monde,
Pour un QCM de ce type, surtout si on est pressé par le temps, aucun calcul n'est vraiment nécessaire.
Une poisson de paramètre lambda devient quasiment symétrique à partir de lambda=10.
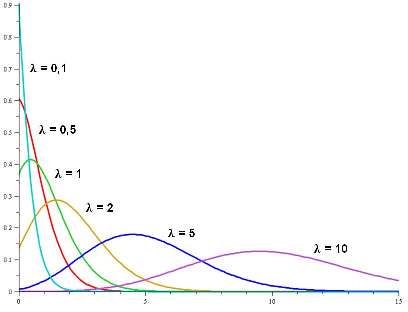
Donc pour une poisson(20), il y a grosso modo 50% de probabilités d'avoir n<20.
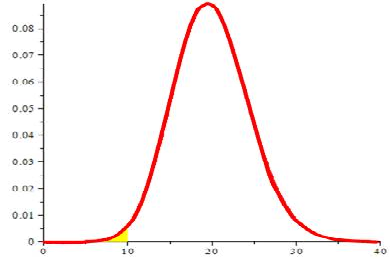
Vu que la distribution commence en 0, et vu sa forme en cloche...
... il est évident géométriquement que la probabilité de n<10 est très nettement inférieure à 10%.
Et la seule réponse valable dans ce cas est la réponse E.
