bonjour,

Ben justement, ça me donne 0/0
Car  

donc je reste bloquée

j'ai oubliée le -2 dans la première équation au numérateur après le 1-x, car f(0)=2

Moi je trouve -1

mais, pourquoi -1? ou est mon erreur?

En fait je cherche la limite non pas de mais

soit lim

en utilisant les limites composées avec la fonction inverse j'en déduit que soit -1

Ah, merci beaucoup, je comprends mieux

> A320

J'ai peur que tu commettes la même erreur qu'ici : Calcul d'une asymptote. Tu ne peux pas remplacer en cours de route un terme par sa limite en laissant les autres (d'ailleurs sur le lien que je viens de donner, tu n'as pas répondu à ma dernière question.)

Pour la limite en question dans cet exercice ici c'est -1/2

Bonsoir,

En reprenant la forme du post de Labo :
f(x) = (e^x-1)/x + 1 - x
f(0) = 2
donc
f(x)-f(0) = (e^x-1)/x - 1 - x
et donc
(f(x)-f(0))/x = ((e^x-1)/x - 1 - x)/x
On on a (e^x-1)/x = (e^x - e⁰)/(x-0)
quand x  -> 0, ce terme tend vers la valeur de la dérivée de e^x en 0, et cette valeur est 1
Finalement,
(f(x)-f(0))/x -> (1 - 1 - x)/x = -x/x
(f(x)-f(0))/x -> -1
Je suis donc d'accord avec A320

--> littleguy
Au temps pour moi, tu as raison ! Il fallait écrire :
(e^x-1)/x 1+x/2
Mais cela provient de e^x 1+x+x²/2, comment justifier cela en Terminale, où on ne pratique pas encore les développements limités ?

Bonsoir LeHibou

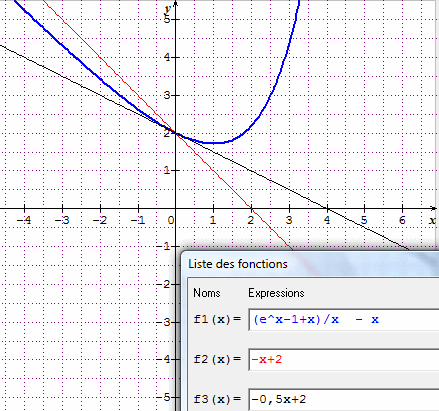
Mais ça ne colle pas avec le graphique : je ne vois pas bien la droite de pente -1 tangente à la courbe au point de coordonnées (0,2)

merci pour le post, je l'avais en effet lu et sur le forum mathematique.net avait eu un autre contre exemple.

Je fini par avoir un gros doute

pour le dénominateur



comme lim f(x)/g(x)=lim f(x)/lim g(x) ici je recompile

Ou est l'erreur?

Je n'avais pas vu ta seconde réponse LeHibou.

Moi non plus je ne vois pas pour l'instant au niveau Terminale. La nuit porte conseil

--> A320
L'erreur est subtile, et difficile à voir en Terminale.
Dans une première approche, comme je l'ai fait, on écrit que (e^x-1)/x - 1 tend vers 0, et il reste donc -x.
En réalité, il faut voir de quelle façon (e^x-1)/x - 1 tend vers 0, et un outil étudié seulement en Maths Sup (les développements limités) permet de répondre à la question.
Pour t'en donner une idée, on démontre que, lorsque x est proche de 0, on peut approximer e^x, non pas par 1+x comme tu as déjà dû le voir, mais par par 1+x+x²/2, et c'est ce terme supplémentaire x²/2 qui va faire toute la différence.
On a alors :
(e^x-1)/x - 1 - x (1+x+x²/2 - 1)/x - 1 - x 1 + x/2 - 1 - x -x/2
et donc :
((e^x-1)/x - 1 - x)/x -> -1/2
Mais pour l'instant je ne vois pas, et littleguy semble d'accord avec moi sur ce point, comment arriver à ce résultat sans l'outil des développements limités...

Je suis preneur pour une vision de mon erreur subtile, parce que là je devient chèvre.

En effet je viens et par un traceur et par le d.l que le résultat est -1/2

voilà un très bon type d'exo pour lever les erreurs subtiles

Je fais tout avec la regle de l'hopistal qui n'est jamais apprise et je ne comprends pas pourquoi. Je crois qu'en fait historiquement il n'en est pas l'auteur mais avait payé un "negre " pour avoir un petit theoreme...
Quoiqu'il en soit pour les formes indeterminées 0/0 ou/ c'est génial.
Si on a f(x)/g(x) qui fait 0/0 alors la limite en 0 sera f'(0)/g'(0) je dérive en haut et en bas et c'est tout puis je fais x=0 !
Ainsi je vois bien que la fonction initiale tend vers 2 qd x tend vers 0.
Démo:
(e^x+1)/1 -x tout ca fait 2 si x=0. La fonction est continue (aussi bien a droite qu'a gauche).
Passons a la derivée:
F'(x)= [(e^x+1)x - (e^x-1+x)]1/x² - 1
= (xe^x+x-e^x+1)/x²  - 1
= (xe^x-e^x+1)/x² - 1
Ce qui conduit encore à une forme indéterminée pour le premier terme 0/0
J'applique l'hospital:
F'(0)= [e^x+xe^x-e^x]/2x - 1
     = [xe^x]/2x -1
     = e[sup]x[/sup/2 - 1 = -1/2 comme coefficient directeur fe la tangent en (0,2)
Ce qui est bien la ligne noire du graphisme.

Effectivement, merci bamboum, l'Hospital est LA solution en Terminale...

Sur l'aspect historique, c'est Jean Bernoulli (il faut bien préciser le prénom, car c'était toute une famille de matheux), voir la section correspondante dans ce lien :

Et sur la famille des Bernoulli :

... Oui ; sauf que l'Hospital n'est "en principe" pas vu je crois en Terminale (en France)

Bonjour
je confirme Littleguy ( 11;10) je pense que ce sujet est extrait d'autres questions avec encadrer exp(x)-x-1par x²/2 et x²/2+x^3/6 ( ordre pas pareil selon le signe de x) pour conclure que la lim cherchee est -0.5

enfin ca doit etre si x<0

et si x>0

Bonjour sloreviv

Tu as sans doute raison ; cette question ne devait pas être isolée, mais précédée d'autres permettant de conclure.

cornelia93 nous le dira peut-être ...

Quelqu'un aurait il des precisions sur ce L'hopital (naissance, lieu ) car dans ma ville il y a des rues avec ce nom  ( prenom: Michel??)

Normal, il est né dans le "63" :

c'est bon Wikipedia m'a repondu  c'est la meme famille! par contre je ne savais pas que la regle de L'H. etait en fait un travail de J.Bernoulli

Mais ce n'est pas le même... :

la derniere ligne de mon msg de 11.57 est a prendre sur [0;ln(3)] pour eviter de dire des betises.

Avant de démontrer que f est dérivable en O, je devait juste donner son domaine de définition.
Donc du coup si j'ai bien compris, le nombre dérivé en 0 est -1/2 et non -1?

Bonjour,

On peut "bricoler":



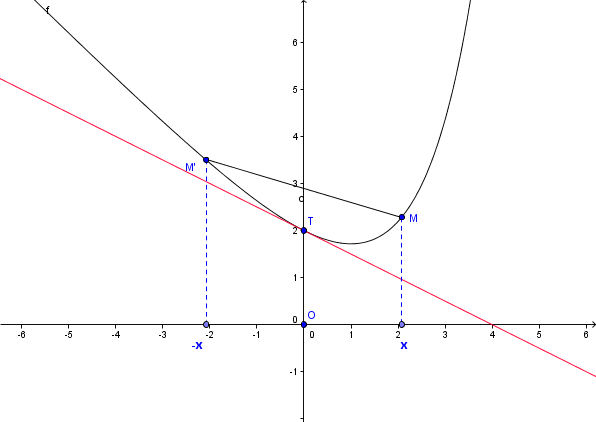
On considère les deux points et de la courbe d' abscisses et

On calcule ensuite le coefficient directeur de la corde :



On considère -c' est là où on "bricole"- que le coefficient directeur de la tangente au point est la limite du coefficient directeur de la corde quand

et

Ah pas mal comme méthode

Merci à tous pour cet exercice:D

Il n' est pas sûr que ce soit une méthode valable pour prouver que est dérivable en 0.

J' aimerais bien que les autres intervenants se prononcent...

Bonjour cailloux

Ton approche me fait penser à l'approche de la vitesse instantanée par les physiciens (voir ). Le lien me semble bien expliquer la "nuance" entre les deux approches "mathématique" et "physique".

Et je ne vois toujours rien de "mieux".

cornelia93 : d'où est issu ton exercice ?

Bonjour littleguy,

Ah oui, ça y ressemble beaucoup!

Merci pour le lien

Bonjour cailloux
Bonjour littleguy,
idem pour le coût marginal

Re bonjour Labo,

Je crois que ce n' est pas tout à fait la même chose.

Dans le lien donné par Littleguy, apparait la notion de dérivée symétrique avec ceci:

Si est dérivable en , alors elle admet une dérivée symétrique en .

Et la réciproque semble fausse.

Ce qui fait qu' avec la méthode employée au dessus (qui revient au calcul d' un "nombre dérivé symétrique" en 0), il est seulement prouvé que admet une dérivée symétrique en 0 mais pas qu' elle est dérivable en 0.

Au mieux, c' est juste une méthode permettant de calculer une limite un peu tordue avec des moyens de Terminale.

Cette méthode est proposée dans le sujet de Bac Réunion 2007 (Exercice 3): Bac S - La Réunion - Juin 2007

  Bonjour  cailloux
merci pour ta réponse et  pour l'énoncé...

Mon exercice est issu d'une annale pour un concours de la fonction publique

> cornelia93

Je ne connais le niveau de mathématiques exigé pour le concours en question. Bac ? Bac+1 ? Est-ce un concours "pour matheux" ou "généraliste" ?

Cela peut dépendre aussi de l'année au cours de laquelle il a été posé (les programmes ont évolué)

Un petit lien utile sur l'île (dû à Nicolas_75) pour d'autres limites : limite d'une fonction en 0

A toi de voir dans les différentes réponses de ce topic (donnant -1/2) ce qui te convient le mieux...

Le niveau en mathématique n'était pas indiqué, mais par contre il y avait le programme en maths :
· notions sur les ensembles ;
· opérations élémentaires sur les ensembles ;
· relations binaires, applications, fonctions ;
· puissance et notions d'exposant ;
· extensions de la notion d'exposant ;
· notions sommaires sur l'inverse de l'exponentiation et le passage aux logarithmes ;
· progressions arithmétiques et géométriques ; intérêts composés ;
· fonction puissance ;
· fonctions exponentielles et logarithmiques ;
· fonctions numériques d'une variable réelle ;
· étude des variations d'une fonction, dérivées, notation différentielle. Formule des accroissements finis;
· intégrales simples : interprétation géométrique ;
· suites numériques, séries numériques : séries à termes positifs, séries titleernées, séries entières,
développements en séries entières ;
· maximums et minimums;
· algèbre linéaire

Mais j'ai fais cet exercice c'était il avait l'air de ressembler au sujets types bac sur les analyse de fonctions.

Bonjour à tous,

Heureux de constater que A320 a compris où était son erreur.

J'ai peut-être une solution mais je ne vais pas tout rédiger parce que c'est un peu lourd.


Alors:

Soit:









Bon c'est ça que je prouve pas (ça se fait en dérivant trois ou quatre fois la fonction différence)

Si x<0:

Si x=0:

Si x>0:

Donc:

Pour tout x<0:

Pour tout x>0:


Donc:

Pour tout x<0:

Pour tout x>0:

Donc:

Pour tout x<0:

Pour tout x>0:


Puis théorème des gendarmes. Et ça marche la dérivée est bien:

oui thiblepri, mais cornelia93 n'a aucune aide dans son exercice et doit le traiter "brut" et le "programme" du concours est un peu vague (la méthode que tu indiques nécessite une certaine familiarité pour introduire les fonctions auxiliaires que tu indiques).

merci d'avoir répondu

Euh ouais... Mais à un niveau terminale un peu poussé, je pense que c'est ce qu'on peut attendre, non?

"un peu poussé", comme tu dis

En même temps, l'exercice n'est pas vraiment simple... Et à mon avis la question est consécutive à quelques autres, non?

Il faut le voir !

trivisteamis, tout aussi mystérieux que littleguy.

Au faite, bonjour littleguy et à tout le monde aussi.

Non. Juste l'ensemble de définition (c'est pour ça que je te précisais qu'il fallait "tout lire" : regarde les posts d'hier entre 11:43 et 14:40)

Ouais, donc chaud! J'avais tout lu _{en diagonale}

Donc à part ma proposition... Je vois pas de truc simple.

Bon les gars je fais le juge. Qui est l'accusé ? Et la partie civile ?

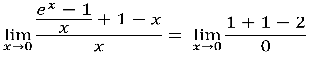
Y'a aucun souci :d