Inscription / Connexion Nouveau Sujet
dans le triangle OKM rectangle en M, que peux-tu dire des angles en O et en M ?
Philoux
s'ils sont complémentaires, que peux-tu en déduire sur leur sinus et cosinus ?
Philooux
Je ne me souviens pas avoir appris quelque chose concernant les sinus et cosinus d'angles complémentaires. Mais j'ai sous les yeux un tableau avec 30, 45 et 60° et leurs cosinus, sinus et tangentes respectifs ; or, cos 30° = sin 60° = 1/2. Donc je suppose que le cosinus et le sinus d'angles complémentaires sont égaux deux à deux, d'où cos KOH = sin KMO. C'est ça ?
sans t'en souvenir
sin(pi/2 - x) = ...
( je ne sais pas si tu l'as déjà vu, par contre )
Philoux
Si cos KOH = sin KMO, alors OH/OK = OK/OM. Les produits en croix sont égaux donc : OK² = OHxOM
Remplacer OK et OM par les valeurs précédemment obtenues et conclure.
On a obtenu aucune valeur dans cet exo, non ?
Cette feuille d'exercices porte sur les différentes moyennes et il y a à chaque fois une "application géométrique". Les valeurs ont sans doute été obtenu dans l'"application géométrique" précédente, à savoir "Moyenne géométrique" (que je n'ai pas fait).
...
Application géométrique 1er épisode (moyenne arithmétique) m = (a+b)/2 :
Sur la droite graduée et orientée d'origine O, A et B sont les points d'abscisses respectives a et b. Que représente le point M d'abscisse m pour les ponits A et B ? A partir de la figure, expliquer les propriétés qui ont permis la construction du point M d'abscisse m = (a+b)/2.
Application géométrique 2eme épisode (moyenne géométrique) g = Vab :
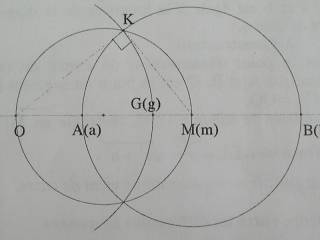
On construit la tagente [OK] en K au cercle de centre M passant par A et B. Le point G cherché est le point du segment [AB] tel que OG = OK. Pouruqoi a-t-on construit le cercle de diamètre [OM] pour obtenir le point K ? En utilisant le théorème de Pythagore dans le triangle OMK rectangle en K et les égalités de longueurs nécessaires, montrer que Ok² = OA x Ob, ce qui permet de conclure.
Application géométrique 3eme épisode (moyenne harmonique) h = 2ab/(a+b) :
Le point cherché est la projection orthogonale du point K sur la droite (AB). Exprimer cos KÔH en fonction des longueurs des côtés dans le triangle OHK rectangle en H. Exprimer sin KMO en fonction des longueurs des côtés dans le triangle OKM rectangle en K.Justifier que cos KÔH = sin KMO. Déduire de cette égalité que OK² = OH * OM. Remplacer OK et OM par les valeurs précédemment obtenues et conclure. Montrer que le point H du segment [AB] vérifie aussi la condition OA/OB = HA/HB (transformer l'égalité en utilisant les abscisses des points et retrouver h = 2ab/(a+b) ).
Application géométrique 4eme épisode (moyenne quadratique) q = V2/2 x V(a²+b²) :
L est le point d'intersection du cercle de centre M passant par A et B. Q est le point du segment [AB] tel que OL = OQ. En utilisant le triangle OML rectangle en M, montrer que l'on a bien OL = V2/2 x V(a²+b²).
Je ne vois pas où des valeurs ont été "précédemment obtenues" 
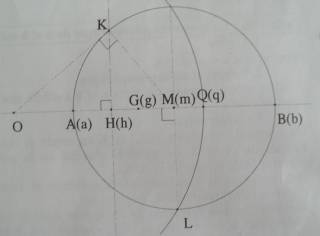
Voici la figure finale :
Moyenne géométrique :
Pourquoi a-t-on construit le cercle de diamètre [OM] pou obtenir le point K ?

En utilisant le théorème de Pythagore dans le triangle OMK rectangle en K et les égalités de longueurs nécessaires, montrer que Ok² = OA x Ob, ce qui permet de conclure.
Dans OMK rectangle en K, on a : KM² + OK² = OM² donc OK² = OM² - KM².
Je ne vois pas comment en à arriver à OK² = OA x OB 
Salut Estelle
tu en es où ?
rappelle ci-dessous ce que tu cherches
Philoux
Salut Philoux, et merci de te re-interesser à mon problème (surtout que je sais que tu es très sollicité)
(14:45)
Application géométrique (moyenne géométrique) g = Vab :
On construit la tagente [OK] en K au cercle de centre M passant par A et B. Le point G cherché est le point du segment [AB] tel que OG = OK. Pouruqoi a-t-on construit le cercle de diamètre [OM] pour obtenir le point K ? En utilisant le théorème de Pythagore dans le triangle OMK rectangle en K et les égalités de longueurs nécessaires, montrer que Ok² = OA x Ob, ce qui permet de conclure.
Pourquoi a-t-on construit le cercle de diamètre [OM] pou obtenir le point K ?

En utilisant le théorème de Pythagore dans le triangle OMK rectangle en K et les égalités de longueurs nécessaires, montrer que Ok² = OA x Ob, ce qui permet de conclure.
Dans OMK rectangle en K, on a : KM² + OK² = OM² donc OK² = OM² - KM².
Je ne vois pas comment en à arriver à OK² = OA x OB.
Je dois t'avouer que je m'y perd un peu
on a démontré que OK²=OH.OM
et, si je comprends bien, il faut pouvoir démontrer que ce OH.OM vaut OA.OB à l'aide de résultats obtenus précédemment 
Je t'avoue mon incompétence, mais suis certain que d'autres mathîliens plus "géométriques" qu'"analytiques"sauront t'aider...
Bon courage !
Philoux
on a démontré que OK²=OH.OM
et, si je comprends bien, il faut pouvoir démontrer que ce OH.OM vaut OA.OB à l'aide de résultats obtenus précédemment
C'est exactement ça.
Merci beaucoup Philoux de ton aide depuis le début.
Est-ce que tu peux par contre me dire pourquoi on a tracé le cercle de diamètre [OM] pour trouver K ?
on l'a tracé pour pouvoir "facilement" obtenir la moyenne géométrique
Philoux
euh... je ne peux pas mettre ça sur ma feuille ^^
Je ne comprends pas pourquoi est-ce plus facile pour obtenir la moyenne ?
je reprend pour t'éclaircir les idées 
tu as 2 nombres a et b positifs
tu les places sur une droite d'origine O
tu détermines le milieu M de AB => m est la moyenne (M comme moyenne arithmétique) de a et b
tu traces le cercle de diamètre AB ( et de centre M donc)
tu traces la tangente à ce cercle issue de O => point K
tu reportes OK avec ton compas pour obtenir G
G comme moyenne Géométrique
ai-je été clair ? 
Philoux
Oui très clair.
D'après tes explications et avec K a pour abscisse k
K est le point d'abscisse la moyenne géométrique de a et b soit d'abscisse V(ab)
Puisque 0<a<b, alors k² = ab. On sait que K n'est pas sur la droite donc K différent de k.
A partir de k² = ab, on doit pouvoir en arriver à OK² = OA x OB.
...mais je ne sais pas comment.
ce qui pose problème, c'est le passage OK²=OH.OM en OK=OA.OB avec l'énoncé que tu as.
le reste n'est que déductif
si tu as OK²=OA.OB => k²=a.b => g=Vab
Attention, ne confond pas K qui est sur la tangente et G qui est entre A et B
Philoux
Tu as raison, je me suis trompée.
K est le point d'abscisse
Puisque 0<a<b, alors k² = ab. On sait que K n'est pas sur la droite donc K différent de k.
Ce n'est pas le point K qui a pour abscisse la moyenne géométrique de a et b soit d'abscisse V(ab).
La moyenne géométrique de a et b soit d'abscisse V(ab) est la distance OK.
Donc OK = V(ab) puisque 0 < a < b, alors OK² = ab. Comme A et B sont sur la droite (OK), alors a = OA et b =OB. Ainsi, OK² = OA x OB.
Est-ce que tu penses que ce raisonnement est le bon ?
oui; simplement, tu dis que OK=Vab (puisque OA=a et OB=b)
et, en reportant par rotation de compas, ce OK vers OG, tu as ainsi le point G situé en moyenne géométrique de A et B...
Philoux

Je suis obligée de répondre à la question même si on est pas obligé de passer par là pour trouver G.
Pour revenir au pb initial :
Si cos KOH = sin KMO, alors OH/OK = OK/OM. Les produits en croix sont égaux donc : OK² = OHxOM
Remplacer OK et OM par les valeurs précédemment obtenues et conclure.
On a obtenu aucune valeur dans cet exo, non ?
Comment faire ?
Estelle, c'est la même question que tu poses depuis 2 heures, sous des formes différentes 
A voir le poids de ce post, je crains qu'un autre mathîlien n'ose s'aventurer pour décrypter le problème...
Un, ou une courageuse (je pense à Youpi  ) peut-être...
) peut-être...
Philoux
Estelle, c'est la même question que tu poses depuis 2 heures, sous des formes différentes 
 ...
...
A voir le poids de ce post, je crains qu'un autre mathîlien n'ose s'aventurer pour décrypter le problème...
Un, ou une courageuse (je pense à Youpi ) peut-être...
Oui, Youpi serait la bienvenue...
Je veux bien essayé de t'aider (même si je ne vais pas pouvoir rester encore très longtemps sur le forum) mais vu la longueur du Topic je suis un peu perdu je dois avouer.
que cherches tu exactement ?
Faut-il vraiment que je lise tout depûis le début, parce que je me sens pas vraiment le courage !
Application géométrique 1er épisode (moyenne arithmétique) m = (a+b)/2 :
Sur la droite graduée et orientée d'origine O, A et B sont les points d'abscisses respectives a et b. Que représente le point M d'abscisse m pour les ponits A et B ? A partir de la figure, expliquer les propriétés qui ont permis la construction du point M d'abscisse m = (a+b)/2.
Application géométrique 2eme épisode (moyenne géométrique) g = Vab :
On construit la tagente [OK] en K au cercle de centre M passant par A et B. Le point G cherché est le point du segment [AB] tel que OG = OK. Pouruqoi a-t-on construit le cercle de diamètre [OM] pour obtenir le point K ? En utilisant le théorème de Pythagore dans le triangle OMK rectangle en K et les égalités de longueurs nécessaires, montrer que Ok² = OA x Ob, ce qui permet de conclure.
Application géométrique 3eme épisode (moyenne harmonique) h = 2ab/(a+b) :
Le point cherché est la projection orthogonale du point K sur la droite (AB). Exprimer cos KÔH en fonction des longueurs des côtés dans le triangle OHK rectangle en H. Exprimer sin KMO en fonction des longueurs des côtés dans le triangle OKM rectangle en K.Justifier que cos KÔH = sin KMO. Déduire de cette égalité que OK² = OH * OM. Remplacer OK et OM par les valeurs précédemment obtenues et conclure. Montrer que le point H du segment [AB] vérifie aussi la condition OA/OB = HA/HB (transformer l'égalité en utilisant les abscisses des points et retrouver h = 2ab/(a+b) ).
Application géométrique 4eme épisode (moyenne quadratique) q = V2/2 x V(a²+b²) :
L est le point d'intersection du cercle de centre M passant par A et B. Q est le point du segment [AB] tel que OL = OQ. En utilisant le triangle OML rectangle en M, montrer que l'on a bien OL = V2/2 x V(a²+b²).
Nous en sommes à moyenne géométrique (2eme épisode) :
Si cos KOH = sin KMO, alors OH/OK = OK/OM. Les produits en croix sont égaux donc : OK² = OHxOM
Remplacer OK et OM par les valeurs précédemment obtenues et conclure.
Et parallèlement à moyenne harmonique :
" on a démontré que OK²=OH.OM
et, si je comprends bien, il faut pouvoir démontrer que ce OH.OM vaut OA.OB à l'aide de résultats obtenus précédemment "(Philoux)
Desole, bonjour d'abord.
OK^2 = OM^2 - KM^2 or KM = AM
donc OK^2 = OM^2 - AM^2 = (OM - AM)*(OM+AM)= OA*OB
Désolé mais j'ai quelques contrainte qui m'oblige à te laisser pour le moment (bébé qui pleure).
Mais j'éssaierai de repasser tout à l'heure
Merci beaucoup Minkus !!
C'est très sympa de ta part.
Il me reste maintenant les moyenes géométrique et quadratique à faire.