Inscription / Connexion Nouveau Sujet
nombre complexe
Bonjour je bloque sur une question:
Vérifier que pour tout complexe z différent de 1, M'(f(z)) appartient à l'axe (OV) si et seulement si M appartient au cercle T de diamètre [UA]
Données de l'exercice:
f(z)=z'=(z-2i)/(z-1)
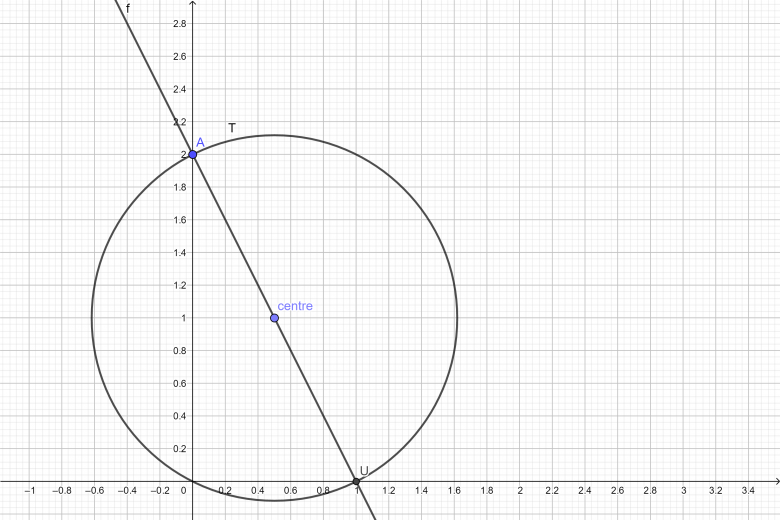
équation du cercle T que j'ai trouvé : (x-0)(x-1)+(y-2)(y-0)=0
l'axe (OV) est l'axe des imaginaires purs
A(0, 2) et U(1, 0)
Merci d'avance
Salu
Ton équation de cercle n'en est pas une
Un cercle c'est (x-xA)^2 +(y-yA)^2=r^2
Qui donne centre A(xA,yA) et rayon r
Commen tu arrives à ton équation ?
j'ai utilisé un prérequis du prof qui est:
L'ensemble des points du plan M(z) vérifiant le vecteur AM fois le vecteur BM = 0 est le cercle de centre [AB]. La traduction analytique de ce produit scalaire donne une équation du cercle. Elle est donc de la forme (x-xb)(x-xb)+(y-ya)(y-yb)=0
alors tu connais l'équation générale d'un cercle (je crois que c'est vu en 1ere)
(x-xA)² +(y-yA)²=r²
le prerequis de ton prof c'est sur le cas des vecteurs
bref
M' appartient à Ov signifie que z' est comment ?
Bonjour à tous les deux
oui ciocciu, en 1re
alexandre0111 ![]() Equation de cercle
Equation de cercle
jsp mais z'=(z-2i)/(z-1) et on va dire que z=a+ib et on sait que a et b doivent 'rentrer' dans (a-0,5)²+(b-1)²=1,25
oulà non rien à voir
z=x+iy (je te conseille de prendre cette forme plutot que a+ib car pour les équations c'est plus simple )
calcule z' sous forme algébrique donc A+iB avec A et B qui dépendront de x et y bien sur
salut,
"Bonjour je bloque sur une question: "
peux tu donner l'enonce en entier ?
on pourrait ainsi comprendre ce que veut ton professeur
Voici l'énoncé en entier:
Problème. Pour tout nombre complexe 𝑧 différent de 1, on pose 𝑀(𝑧), 𝑀′(𝑧') avec :
f(z)=z'=(z-2i)/(z-1)
1. Vérifier que si 𝑀(𝑧 = 2𝑖) alors 𝑀′
appartient à l'axe (𝑂𝑈).
2. Vérifier que si 𝑀(𝑧 = −2 + 6𝑖) alors 𝑀′
appartient à l'axe (𝑂𝑈).
On pose 𝐴 (0; 2)
et 𝐵(-2; 6)
3. Vérifier que si 𝑀(𝑧) appartient à la droite (𝐴𝐵) alors 𝑀′
appartient à l'axe (𝑂𝑈). Étudier la réciproque.
4. Vérifier que si 𝑀(𝑧 = 0) alors 𝑀′
appartient à l'axe (𝑂𝑉).
5. Vérifier que si 𝑀(𝑧 = 2𝑖) alors 𝑀′
appartient à l'axe (𝑂𝑉).
6. Donner l'équation du cercle T de diamètre [𝑈𝐴].
7. Vérifier que pour tout nombre complexe 𝑧 différent de 1, 𝑀′(𝑓(𝑧)) appartient à l'axe (𝑂𝑉) si et seulement
si 𝑀 appartient au cercle T.
ok c'est quoi ta réponse à la 6 ? en tenant compte de ce que je t'ai raconté sur l'équation d'un cercle
c'est bon j'ai trouver ciocciu m'a mit sur la piste en mettant z' sous la forme algébrique merci à vous et bonne soirée