- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Nombre complexe - Translation de repère
Bonjour à tous,
Je suis actuellement confronter à un problème que je n'arrive pas à résoudre.
Je précise que ce n'est pas un devoir que je dois faire en cours.
Je possède un nombre complexe (ex a = 3+3i) dans le repère cartésien. Ensuite un second nombre complexe (ex b = 4+3.5i).
Je décide ensuite, d'établir un "périmètre" de rayon R ayant pour centre 3+3i.
Le nombre 4+3.5i se trouve donc à l'extérieur du cercle de centre 3+3i.
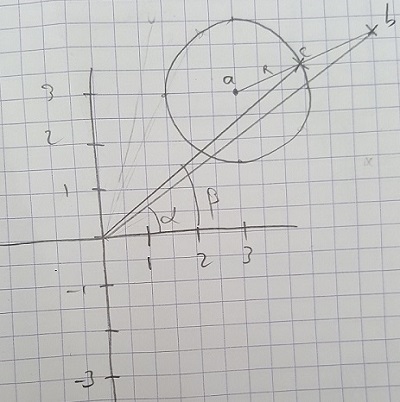
Par la suite, je désire avoir les coordonnées du point c situé sur le cercle de centre a et de rayon r mais ayant le même argument que le nombre b.
Illustration ci-joint.
En outre, si a était le centre du repère il aurait été simple de trouver les coordonnées du nouveau point : xc = R*cos(arg(a)) et yc = R*sin(arg(a)).
Cependant je dois les trouver avec comme repère le repère cartésien dont le point a n'est pas le centre.
Je ne sais pas si je me suis bien fais comprendre 
Merci à tous ceux qui pourront m'aider.
salut
si O est l'origine du repère cartésien alors
quant au point C il s'obtient aisément comme
....
Le point c doit être sur la même demie droite [O, b[ car b et c ont le même argument.
Vous avez deux points de rencontre entre le cercle et la demi droite [O, b[ qui sont des solutions possibles.
Bonjour
tu veux que c ait le même argument que b ? ce n'est pas ce qui apparaît sur tes figures, pourtant ?
Merci carpediem pour ta réponse.
Cependant mon but est d'obtenir les coordonnées du point C, comment les avoir ?
Même avec la relation vectorielle que tu as écrite, comment avoir ses coordonnées sachant que seules ces informations sont connues :
coordonnées du point a, b, et le rayon R.
a pour coordonnées
idem pour en remplaçant tous les C par des B
et
tu es vraiment en master  rassure moi : pas de maths ?
rassure moi : pas de maths ?
Bonjour ,
sans être sur d'avoir compris ton énoncé , il y aurait 2 repères (un de centre a et un de centre disons O)
Les coordonnées de c dans le repère O sont celles de c dans le repère a (que tu as données) plus les coordonnées de a dans le repère O .
Cordialement
Le point c que vous proposez ainsi que carpediem n'a pas le même argument que le point b comme demandé dans l'énoncé.
Le point
En fonction de la valeur de r vous avez pour c soit :
- 0 point solution dans le cas où OB ne touche pas le cercle
- 1 point solution dans le cas où OB est tangent au cercle
- 2 ponts solutions dans les autres cas
si C appartient à la droite (AB) alors :
salut
si O est l'origine du repère cartésien alors
quant au point C il s'obtient aisément comme
....
donc
donc avec des complexes :
Merci lafol. En effet comme à dit fm_31, lorsque je parlais d'argument je parlais dans le repère de centre A.
Oui lafol plus de maths depuis 2 ans malheureusement..
Merci pour vos réponses je reprendrai mon problème demain et vous tiendrai au courant.
Le résultat proposé par carpediem 03-05-16 à 16:32 est bon. Il reste un détail et de taille, c'est que , ceci nous donne une contrainte sur R ce qui entraine l'étude des trois cas que j'avais signalé.
Cependant pour qu'il y ait le même argument on ne prendra pas le cas où il y ait 2 points solutions.
Aussi on considère OB touchera le cercle.
Le point c est quelconque sur le cercle.
Excusez moi, je me suis trompé de jugement.
La relation n'est pas justifié car
ne fait pas partie de
mais plutôt de
si solution il y a.
Razes : l'argument c'était une erreur ....
Merci lafol. En effet comme à dit fm_31, lorsque je parlais d'argument je parlais dans le repère de centre A.
Oui lafol plus de maths depuis 2 ans malheureusement..
Merci pour vos réponses je reprendrai mon problème demain et vous tiendrai au courant.
salut
je trouve ( à verifier )
Xc = 3 + 2.R/ 5
5
Yc = 3 + R/ 5
5
pour que Le nombre 4+3.5i se trouve à l'extérieur du cercle de centre 3+3i.
il faut que Xc < 4 et Yc < 3,5
on a donc 3 + 2.R/ 5 < 4 donne R <
5 < 4 donne R < 5/2
5/2
et 3 + R/ 5 < 3,5 donne R <
5 < 3,5 donne R < 5/2 ... donc la meme
5/2 ... donc la meme
chose
Le résultat proposé par carpediem 03-05-16 à 16:32 est bon. Il reste un détail et de taille, c'est que
c'est incompatible ... sauf si A, B et C sont alignés ....
donc les deux hypothèses conduisent à un énoncé faux ....
Carpediem, justement a, b et c sont aligné. Peu importe le point c et le point b, les 3 points doivent être alignés.
oui mais ton énoncé devient foireux lorsque tu imposes arg (c) = arg (b)
Par la suite, je désire avoir les coordonnées du point c situé sur le cercle de centre a et de rayon r mais ayant le même argument que le nombre b.
ou alors c'est une autre question (plus difficile) mais qui ne correspond pas à tes figures ...
@Carpediem
J'ai eu le même réflexe concernant mais lafol m'a rappelé la réponse de graindri à 03-05-16 à 16:32. Donc ne pas tenir compte de cette équation.
De ce fait la solution est ce que tu as proposé :



 analyse complexe en post-bac
analyse complexe en post-bac