- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Nombres Complexe
Salut à tous j'ai un exercice à faire, et j'ai du mal à le résoudre, donc le voici :
Soit m  à
à  , trouver une condition nécessaire et suffisante sur m pour que :
, trouver une condition nécessaire et suffisante sur m pour que :
a) ( 3 - i)m
3 - i)m 

b) ( 3 + i)m
3 + i)m  i
i
J'aurai tendance à dire pour la a), il faut que m soit impair et pour la b) pair ? De plus il faut le démontrer...
salut
pour m>0 utilise le binôme de Newton et simplifie les puissances de i pour conclure
pour m<0 calcule d'abord l'inverse puis recommence comme avant
autre méthode : utilise la forme exponentielle....
on reconnait trivialement....
Pour la a) :
Soit :
a =  3
3
b = -i
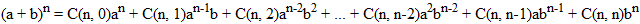
Or :
C(n, 0) = C(n, n)
C(n, k) = C(n, n-k)
On factorise :
= C(n,0)(a^n + b^n) + C(n,1)(a^(n-1)*b + a*b^(n-1) + ... (1)
= 2^n * (-1)^(-n/6) (Fais avec la calculatrice). (2)
Le problème est que je ne sais pas comment faire pour arriver de (1) à (2) ?
Sinon, donc pour que l'équation a) € R il faut que -6  n
n  6 :
6 :
Car on sait que 2^n € Z puisque n € Z, de plus -1 = e^i* , donc (-1)^-n/6 = (e^i*
, donc (-1)^-n/6 = (e^i* )^-n/6 = e^i
)^-n/6 = e^i *-n/6 (3)
*-n/6 (3)
(4) On peut en déduire que pour que e^i *-n/6 € R, il faut que -n/6 € Z donc que n € 6*a avec a appartenant à N.
*-n/6 € R, il faut que -n/6 € Z donc que n € 6*a avec a appartenant à N.
Encore un autre problème entre (3) et (4), il faut que dans mon devoir il y ait de la régularité ou je ne sais pas quoi ect... Car le "on peut en déduire", je sais que mon professeur va me dire, montre moi ta déduction ect...
Merci.
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Ça nous fait donc :
( 3 - i)m = (2 [cos
3 - i)m = (2 [cos  /6 - i sin
/6 - i sin  /6])m = (2 [cos -
/6])m = (2 [cos - /6 + i sin -
/6 + i sin - /6])m = 2^m * [cos -
/6])m = 2^m * [cos - /6 + i sin -
/6 + i sin - /6]m
/6]m
D'après De Moivre :
2^m * [cos - /6 + i sin -
/6 + i sin - /6]m = 2^m * [cos -m
/6]m = 2^m * [cos -m /6 + i sin -m
/6 + i sin -m /6] = 2^m * e^-i
/6] = 2^m * e^-i *m/6 = 2^m * (e^i
*m/6 = 2^m * (e^i )-m/6 = 2^m * (-1)^-m/6.
)-m/6 = 2^m * (-1)^-m/6.
Merci.
Puis pour la b) c'est à peu près la même chose...
Encore Merci. Sinon par curiosité comme vous aurez fait avec le binôme de Newton ?
et pour résoudre ton exercice, la caractérisation des réels et des imaginaires purs par leur argument est le plus efficace ici ....
Merci.
@ Carpediem OUI !!! J'AVAIS DEJA FINIS L'EXERCICE, JE VOULAIS SEULEMENT SAVOIR ce que c'était iR mais c'est bon lol... C'était tout simple...
Encore Merci pour vos réponses.


 S.V.P.
S.V.P.



 analyse complexe en post-bac
analyse complexe en post-bac