Bonjour malou
Tout à fait !

coucou Sylvieg

Bonjour
A est donc sur le cercle

Et il y a combien de points d'intersection de la médiatrice avec le cercle ?

Comme ça

Si je construis la médiatrice de [OA] ,ça donnera OM=AM≠1

Sur ta figure, je ne vois pas la médiatrice de [OA].

Voilà

Quelle fatigue !
Où sont les points d'intersection ?
Quelles sont leurs affixes ?

Difficile de donner leurs parties imaginaire mais leur partie réelle commune est 1/2

Il y a un petit air de cercle trigonométrique, non ?

Et puis, remplacer x par 1/2 dans l'équation du cercle, ça n'est pas insurmontable non plus.

* Trigonométrie

L'abscisse des deux points M1 et M2 (1/2) et le Cosinus des angles π/3 et -π/3 qui ont pour sinus respectifs -√3/2 et √3/2
Donc les points M1 et M2 ont pour affixes z1 = 1/2 +i√3/2 et z2 = 1/2 -i√3/2

*Équation du cercle

Le cercle a pour équation :
x²+y²=1²
(1/2)²+y²=1²
y=√3/2 ou y=-√3/2

Donc les affixes des points M1 et M2 sont z1 = 1/2 +i√3/2 et z2= 1/2 -i√3/2

carpediem
C'est maintenant que je comprends ce que vous aviez dit

Bon alors, maintenant que tu as la réponse, une remarque :
Tu es parti de OM = MA = 1.

Tu as exploité OM = MA (médiatrice) et OM = 1 (cercle de centre 0).

Il y a d'autres manières de trouver les 2 points.
Parmi elles, une compliquée :
Intersection du cercle de centre 0 et de rayon 1 avec le cercle de centre A et de rayon 1.
Et une simple :
OAM est un triangle équilatéral de côté 1 car OA = 1.

Quelle calculs dois je dois effectuer pour ces deux méthodes

La compliquée :
Écrire des équations des cercles et résoudre le système.
Ou sans calcul, un peu de géométrie.

OAM triangle équilatéral :
Les points M sont images du point A dans 2 rotations de cente 0.

Ok
Équation du cercle de centre O et de rayon 1


Équation du cercle de centre A et de rayon 1


Donc

la compliquée c'est ce que tu viens de faire et qui est faux !!! les coordonnées d'un point sont (x, y) épictou !!! que ce soit pour le cercle de centre o comme pour le cercle de centre A !!!

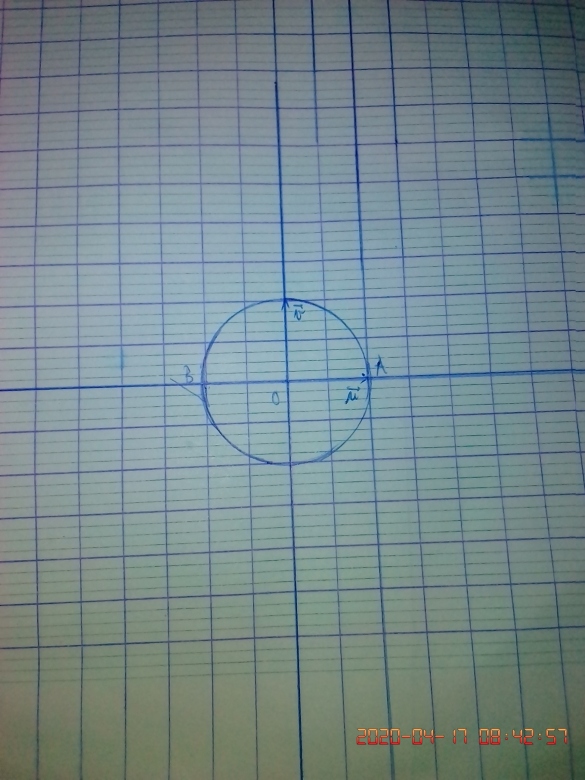
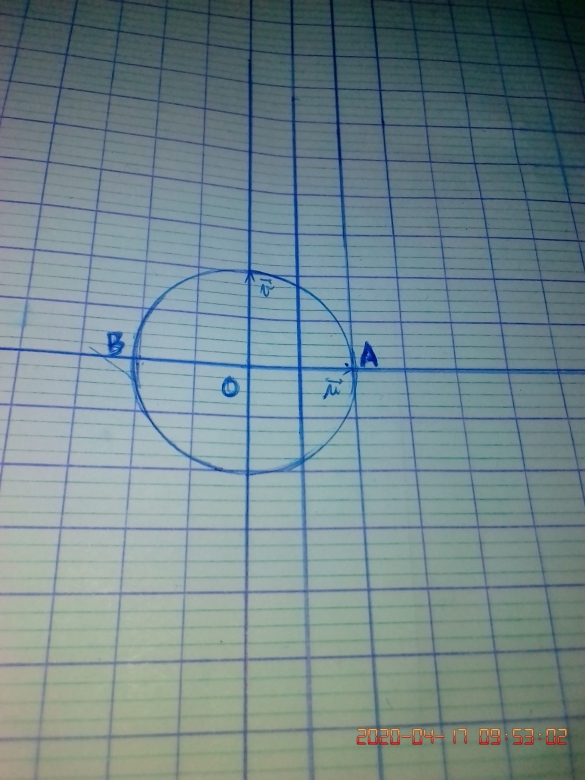
médiatrice deu segment [OA]

cercle C(O, 1)



epictou ...



PS : et même cette histoire de triangle équilatéral et de rotation ça me semble compliqué ...

Bonjour carpediem,
Des rotations de centre O et d'angles de mesure /3, c'est quand même pas la mer à boire.
Surtout quand on cherche l'image du point d'affixe 1

Quant au cercle de centre A et de rayon 1, on pourrait envisager de demander à Samsco d'en écrire une équation (avec du x et du y ...).

Quant à tes équivalences, passer par la géométrie est un détour inutile :

certes ... mais comme on ne voit même plus les rotations géométriquement (que reste-t-il de la géométrie d'ailleurs) si ce n'est que du calcul bestial ...

par contre ils voient les équations de cercle (comme application du produit scalaire)

j'ai préféré resté "dans le programme" dans le cas présent ...

et tu as tout à fait raison en posant la bonne question à Samsco puisque c'est au programme !!!

pour la deuxième ok

pour la première il y a tout de même une petite étape calculatoire  (développer (x - 1)^2 et réduire (bon c'est élémentaire bien sur)

mais je ne suis absolument pas d'accord avec

Sylvieg @ 18-04-2020 à 08:21

Quant à tes équivalences, passer par la géométrie est un détour inutile :

D'accord.

L'équation de cercle de centre A(1;0) et de rayon 1 a pour équation:

(x-1)²+(y-0)²=1²

(x-1)²+y²=1²

D'accord.

Je crois qu'on a terminé .
Merci pour tout !

Ah non ,vous avez parlé de rotation ( que je ne connais pas )

Sans intérêt si ça n'est plus au programme de terminale.

Ok mais j'aimerais connaître quand mm ( j'espère que c'est pas difficile)

Je ne sais pas avec assez de précision ce qui est au programme actuel de terminale S sur les rotations.

et de toute façon il y a internet ... pour déjà voir un peu les choses ...

Ok merci !

de rien