Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

Nombres complexes

Posté par
Samsco 14-04-20 à 10:48

Bonjour j'ai besoin de votre aide svp

Exercice :

1. Déterminer le réel x tel que :

x²-3x+2+i(2x²+x-10)=0

2. Déterminer les complexes z tels que :
|z|=|\dfrac{1}{z}|=|z-1|

3. Soit M d'affixe z=x+iy où x et y sont des réels . On considère le nombre complexe z'=z².

a) Exprimer en en fonction de x et y , les parties réelles et imaginaires de z'.
b) Déterminer et dessinerles ensembles des points M tels que z' soit un réel , puis un imaginaire pur.

Réponses:

x²-3x+2+i(2x²+x-10)=0 \\ \\ x²-3x+2=0\ \text{ou} 2x²+x-10=0 \\ \\ x=2\ \text{ou}  x=1 \ \text{ou} x=2 \ \text{ou}  x=-5/2

2. Soit z=x+iy

*|z|=|z-1| \\ |x+iy|=|x-1+iy| \\ \sqrt{x²+y²}=\sqrt{(x-1)²+y²} \\ x²+y²=x²-2x+1+y² \\ x²+y²-x²-y²=-2x+1 \\ x=\frac{1}{2} \\ \\ * |z|=|\dfrac{1}{z}| \\ \\ |z|²=1 \\ \\ |x+iy|²=1 \\ \\ x²+y²=1 \\ \\ (1/2)²+y²=1 \\ \\ y²=3/4 \\ \\ y=\dfrac{\sqrt{3}}{2} \ \text{ou} y=-\dfrac{\sqrt{3}}{2} \\
Les complexes z tels que :
|z|=|1/z|=|z-1| sont

z_1=\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2} \ \text{et} /z_2=\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 10:49

bonjour

1 : faux dès la deuxième ligne

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 10:51

(A ; B ; A+iB=0) ...?...

Posté par
Samscore : Nombres complexes 14-04-20 à 10:54

z_2=\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}

Posté par
Samscore : Nombres complexes 14-04-20 à 10:55

a+Ib=0 <=> a=0 ou b=0

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 11:03

non !

donc pour toi

1 + 0i = 0 puisque (1=0 OU 0=0)

Posté par
Samscore : Nombres complexes 14-04-20 à 11:09

Qu'est ce que je dois écrire alors?

Posté par
Samscore : Nombres complexes 14-04-20 à 11:16

z=\iff \begin{cases}\left Re(z)=0 \ \right Im(z)=0 \end{cases}

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 11:20

incompréhensible

faut apprendre son cours précisément ...

et mettre les bons connecteurs logiques...

donc je répète :

matheuxmatou @ 14-04-2020 à 10:51

(A ; B ; A+iB=0) ...?...

Posté par
Samscore : Nombres complexes 14-04-20 à 11:23

a+Ib=0 <=> a=0 et b=0

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 11:29

Samsco @ 14-04-2020 à 11:23

a+Ib=0 <=> a=0 et b=0


oui !

Posté par
Samscore : Nombres complexes 14-04-20 à 11:32

Donc (x=2 ou x=1) et (x=2 ou x=-5/2)

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 11:41

ouiiii !

Posté par
Samscore : Nombres complexes 14-04-20 à 11:52

Pour la 2)

C'est juste?

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 12:04

tu n'as toujours pas fini la 1

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 12:05

pour la 2 c'est juste

Posté par
Samscore : Nombres complexes 14-04-20 à 12:05

Qu'est ce que je dois faire ?

Posté par
Samscore : Nombres complexes 14-04-20 à 13:30

C'est bon , j'ai compris x=2

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 13:53

oui

Posté par
Samscore : Nombres complexes 14-04-20 à 13:54

a)
z'=z^2 \\ \\ z'=(x+iy)^2 \\ \\ z'=x^2+2xyi-y^2 \\ \\ Re(z')=x^2-y^2 \text{et}  Im(z')=2xy

b)
* Ensemble des points M tels que z' est réel

\text{z' est réel} \iff Im(z')=0 \\ 2xy=0 \\ xy=0 \\ x=0 \ \text{ou}  y=0 \\ \\ Comment je trouve l'ensemble des points M? \\ \\ \text{z' est imaginaire} \iff Re(z')=0 \\ x²-y²=0 \\ (x-y)(x+y)=0 \\ x=y \ \text{ou}  x=-y

L'ensemble des points M est la réunion des premières et deuxiemes bissectrices

Posté par
matheuxmatoure : Nombres complexes 14-04-20 à 17:18

et dans le premier cas c'est la réunion de quoi ?

Posté par
Samscore : Nombres complexes 15-04-20 à 11:55

Ah oui ,c'est la réunion de l'axe des réels et de l'axe des imaginaires

Posté par
matheuxmatoure : Nombres complexes 15-04-20 à 13:40

oui

Posté par
Samscore : Nombres complexes 15-04-20 à 13:41

Ok merci pour tout

Posté par
matheuxmatoure : Nombres complexes 15-04-20 à 13:45

pas de quoi

Posté par
carpediemre : Nombres complexes 15-04-20 à 19:54

saut

dommage de passer par des calculs pas nécessaires ...

|z| = \left| \dfrac 1 z \right| = |z - 1|

|z| = |z - 1| \iff |z - 0| = |z - 1| et l'interprétation géométrique donne immédiatement le résultat

|z| = \left| \dfrac 1 z\right| et l'interprétation géométrique donne immédiatement le résultat

et on en déduit alors le résultat final ...

3/ si on connait la forme exponentielle c'est encore plus rapide et efficace que la forme algébrique ...

Posté par
Samscore : Nombres complexes 15-04-20 à 20:11

Ah ok
Sinon , comment on peut écrire le conjugué d'un complexe avec le latex?

Posté par
Samscore : Nombres complexes 15-04-20 à 20:16

*|z|=|1/z|
|z|²=1
OM²=1
OM=1

|z|=|z-1|
OM=AM
Avec A d'affixe z_A=1

Posté par
carpediemre : Nombres complexes 15-04-20 à 20:30

donc on arrive immédiatement à (1/2)^2 + y^2 = 1 ...

Posté par
Samscore : Nombres complexes 15-04-20 à 20:33

Je ne comprends pas

Posté par
Samscore : Nombres complexes 15-04-20 à 20:36

OM=AM=1
Donc AOM est un triangle équilatéral de côté 1

Posté par
carpediemre : Nombres complexes 15-04-20 à 20:42

non !!

OM = AM epictou !!!

et l'ensemble des points M tels que OM = AM est ... ?

Posté par
malou Webmasterre : Nombres complexes 15-04-20 à 21:00

Samsco @ 15-04-2020 à 20:11

Ah ok
Sinon , comment on peut écrire le conjugué d'un complexe avec le latex?


\bar z ou \bar {z-1} donne \bar z ou \bar {z-1}

Posté par
Samscore : Nombres complexes 15-04-20 à 23:34

Ok merci !

Posté par
Samscore : Nombres complexes 15-04-20 à 23:34

carpediem @ 15-04-2020 à 20:42

non !!

OM = AM epictou !!!

et l'ensemble des points M tels que OM = AM est ... ?


L'ensemble des points M est la médiatrice du segment [OA]

Posté par
malou Webmasterre : Nombres complexes 16-04-20 à 01:58

ben oui !

Posté par
Samscore : Nombres complexes 16-04-20 à 16:30

Oui mais ça ne m'aide pas les nombres complexes tels que : |z|=|z-1|=|1/z|

Posté par
Sylvieg Moderateurre : Nombres complexes 16-04-20 à 16:38

Pour la question 2), tu as presque terminé avec ceci :

Citation :
*|z|=|1/z|
|z|²=1
OM²=1
OM=1

|z|=|z-1|
OM=AM
Avec A d'affixe z_A=1
Pense à dire que les lignes sont équivalentes dans chaque paquet.

Posté par
Samscore : Nombres complexes 16-04-20 à 16:41

OM=AM=1

Posté par
Sylvieg Moderateurre : Nombres complexes 16-04-20 à 16:43

Où sont les points M qui vérifient ça ?
Réponds avec des phrases s'il te plait.

Posté par
Samscore : Nombres complexes 16-04-20 à 16:51

Ils sont sur la droite qui passe par le milieu de [OA] et qui est perpendiculaire à (OA)

Posté par
Sylvieg Moderateurre : Nombres complexes 16-04-20 à 16:55

Pour OM = AM, tu as répondu ceci :

Citation :
l'ensemble des points M tels que OM = AM est ... ?

L'ensemble des points M est la médiatrice du segment [OA]


Et pour OM = 1 ?

Posté par
Samscore : Nombres complexes 16-04-20 à 17:07

Les points M se trouvent sur le cercle de centre O et de rayon 1

Posté par
Sylvieg Moderateurre : Nombres complexes 16-04-20 à 17:20

Donc les points M sont à l'intersection de ... et de ... .

Posté par
carpediemre : Nombres complexes 16-04-20 à 18:13

tu ne peux pas avancer si tu ne fais que des réponses partielles sans une synthèse complète des résultats et surtout quand on interprète géométriquement sans dire en français proprement ce que signifie les résultats obtenus !!

je te rappelle que tu as déjà obtenu les résultats (dès ton premier post) par le calcul et que je suis intervenu pour te montrer simplement qu'en interprétant géométriquement les résultats tu n'as qu'un calcul de collège à mener (voir mon post de 20h30)

Posté par
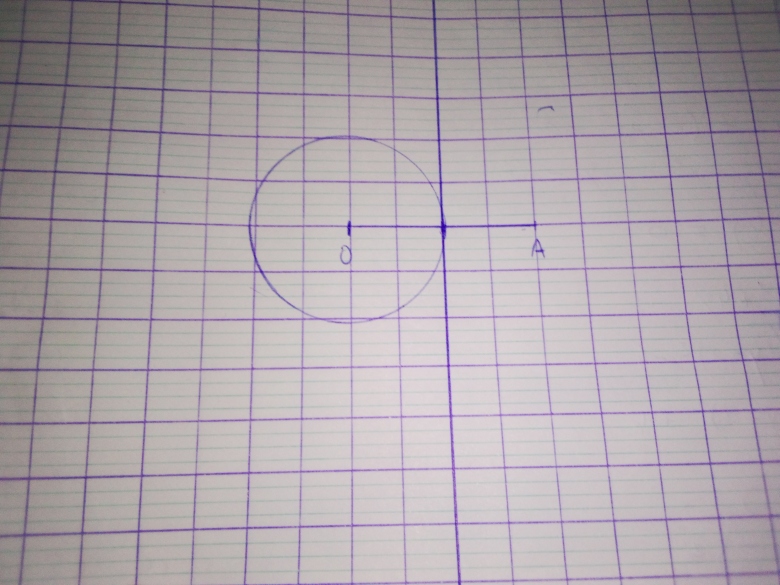
Samscore : Nombres complexes 16-04-20 à 21:03

C'est justement ce que j'ai pas compris ( post de 20h30)

Posté par
Samscore : Nombres complexes 16-04-20 à 21:06

Sylvieg @ 16-04-2020 à 17:20

Donc les points M sont à l'intersection de ... et de ... .


Les points M sont à l'intersection du cercle de rayon 1 et de la médiatrice du segment [OA]

Posté par
Sylvieg Moderateurre : Nombres complexes 16-04-20 à 22:50

As-tu fait une figure ?

Posté par
Samscore : Nombres complexes 16-04-20 à 23:03

En effet

Nombres complexes

Posté par
Sylvieg Moderateurre : Nombres complexes 17-04-20 à 06:29

De bon matin,
Le point A a pour affixe 1 et le cercle a pour rayon 1.
Un des deux est faux.

1 2 +


Rechercher
Menu
Espace membre
11 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !