Salutation,

Après les différentielles tu te mets aux complexes ? ^_^

Le 2i se voit très clairement dans le z -2i non ? Le 2i vient de là.

Y a plusieurs moyens de voir ça.

On peut voir z - 2i comme l'affixe d'un vecteur. Du coup l'égalité |z - 2i| = 2 est juste une égalité qui traduit la longueur d'un vecteur dans le plan complexe.

On peut aussi passé par les coordonnées en posant z = x + iy on a alors |z - 2i| = (x² +(y - 2)²), ce qui permet d'obtenir :
|z - 2i| = 2 (x² +(y - 2)²) = 2 x² + (y -2)² = 4
On reconnait alors l'équation cartésienne d'un cercle de rayon 2 et de centre C de coordonnées (0,2) c'est à dire d'affixe 2i.

Tout se rejoint au final.

En complément. La géométrie du plan rapportée à un repère orthonormé est l'image de l'ensemble des nombres complexes. A chaque point correspond un nombre complexe (affixe) et vice versa.

Comme l'a si bien dit Wataru correspond au point du plan complexe.

Quand on écrit ceci correspond au vecteur ayant pour coordonnées . Quand on note ceci correspond à qui est la distance du point au point

Donc correspond à qui est l'équation du cercle de centre et de rayon .

Toutes les transformations de géométrie (rotation, translation, homothétie, Symétrie, coordonnées cartésiennes, coordonnées polaires, alignement de points, calcul d'angles, ...) sont applicables avec les nombres complexes.

@Wataru : Eh oui ! Et ensuite ça sera les matrices, puis les vecteurs


Donc, si j'ai bien compris vos explications (+ les explications d'un collègue) :

    où (a,b) est le centre de l'équation du cercle.

    où (a,b) est le centre de l'équation cartésienne (complexe).

C'est bien ça ?

Et dans notre cas :


   Donc centre en (0,2)

Pour les complexes, , donc par exemple où le centre est en (3,5), je n'en suis pas certaine ... une correction s'il vous plait ?

oui

Mmh ... Tout allait bien jusqu'au moment ou je rencontre ceci !



Alors là, aucune idée. Le membre de droite je peux comprendre, mais le membre de gauche

Une petite aide s'il vous plait ?

@Wataru ? @Razes ?

Là on va pas pouvoir se contenter de forme générale ^_^

Tu te rappelles de la formule qui donne pour a et b deux complexes (b non nul), |a|/|b| = ... ?

Non, aucun souvenir de ça

Apprend les relations entre modules et les formules sur les arguments aussi... Ca pourrait être pratique =P

Tiens, essaye de démontrer que pour tout a et b complexes on a :

|a|.|b| = |a.b|

A partir de là essaye de démontrer la formule vue plus haut et résout ton exo ^_^

Ah je vois !

Donc si
alors

J'applique ceci et ça me donne :

Bon, est la distance (euclidienne) du point d'affixe à l'origine , n'est-ce pas ?
Et est la distance du point d'affixe au point d'affixe .

Alors, l'ensemble des points équidistants de et de , qu'est-ce que ça peut bien être ?

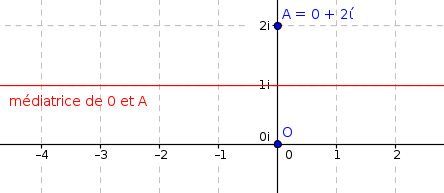
J'ai représenté 2 cercles de même rayon, l'un en (0,0), l'autre en (0,2). Et les seuls points équidistant forme une ligne horizontale en 1i. Possible ou je me goure totalement ?
Si c'est juste, peut-t-on y arriver avec un calcul ? Car j'ai pu trouver (la suite de ma démo étant fausse j'imagine) mais ça ne représente pas grand chose pour moi ... J'aurais donc vraiment besoin d'une petite explication s'il vous plait

Attends, tu ne sais pas ce qu'est la médiatrice de deux points ?

Bien sûr que oui ! Voyons, je ne suis pas nulle à ce point

Lorsque je dis que ça ne représente pas grand chose pour moi, je parle bien de l'équation !

T as l'équation:



Développe l'équation. et simplifie là.

Alors, si tu sais ce qu'est la médiatrice de deux points, tu sais donc que l'ensemble des points d'affixe telle que est la médiatrice de et de , c'est-à-dire la droite des points d'affixe dont la partie imaginaire vaut .
Le titre de ton fil est "plan de Gauss" (on dit souvent plutôt "plan d'Argand"). Ca veut dire qu'on aborde les complexes d'un point de vue géométrique, la géométrie du plan euclidien. Il est donc important de te souvenir de tes connaissances en géométrie, et de les utiliser !
Je parie que ce qui était attendu dans ton exercice, c'était bien une description géométrique de l'ensemble des points d'affixe telle que .

Développe l'équation. et simplifie là.

Hum ... J'aurais surement l'air conne de demandé ça, mais ... Pourquoi l'avoir élevé au carré ?
Aussi, z représente un point en (0,1). Le calcul ne me dit pas que le résultat est une ligne horizontal passant par i, vous comprenez ce que je veux dire ? Je suis un peu perdue ...
Loin de moi l'idée de paraître arrogante, mais j'aurais vraiment besoin d'une explication détaillé, je ne comprend jamais du premier coup

La géométrie a du bon, n'est-ce pas ? On voit mieux ce qui se passe. Enfin, moi je trouve...

Sinon : on élève le module au carré parce que (et )

Erreur de calcul, C'est le module au carré, donc

Désolé, au moment de poster, je n'ai pas vu le message précédent.

Ah oui, juste ! J'ai developpé et j'ai obtenu :

Qui montre clairement une fonction horizontale en 1i !

Je pense avoir compris le truc, j'ai pu faire les 2 autres en procédent comme ceci :

1°) Changer en
2°) Développer l'équation et se rappeler que
3°) Reconnaitre si j'obtient une équation cartesienne (donc sous la forme , ou une fonction constante (comme dans mon exercice : )

Vous confirmez ? (En espérant que ça soit juste !!)

Oui
De plus la géométrie du plan est très importantes à connaitre car cette analogie te facilitera la compréhension.