salut

ce qui serait bien c'est de nous déposer une figure avec le triangle ABC et ses hauteurs et médiatrices, les milieux I, J, K des côtés, O et H ...

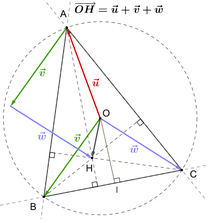
Je me permets de piquer la figure du wikipedia

Ici, je ne voulais pas pas forcément introduire les points milieux des côtés. Juste trouver un vecteur normal à chaque côté pour diriger les hauteurs, en faisant remarquer que des vecteurs directeur des médiatrices font l'affaire! Du coup pour , on a:
  car  

Bonjour,

Bonjour PLSVU.

   Je ne comprends pas votre réponse (par rapport à la question de mon post).  Le point O est la donnée du problème, et j'utilise ses propriétés (OA=OB=OC).

   Bonjourfabo34fabo34

Que dire du point 0 pour le triangle A'B'C' ....

Oui. C'est l'orthocentre. Mais là il me semble qu'on retombe dans les démonstrations "classiques". Dans mon cas, je voulais inviter un élève à utiliser l'outil vectoriel pour contruire des points avec des déplacements, comme lorsqu'on avance dans l'inconnu. Je trouve que la plupart des exos du lycée sont "téléphonés", du moins n'invite guère à la démarche constructive. Je vous renvoie à mon précédent post où on cherche à trouver les courbes qui envoient des rayons issus d'un point dans une unique direction. Classiquement on demande aux élèves de vérifer qu'une solution toute faite, à savoir les paraboles, fonctionne. Je trouve ça beaucoup moins intéressant.

Là dans mon post, j'aimerais juste savoir comment prouver "joliment" que

Juste pour donner un exemple. Je n'ai vu dans aucun manuel scolaire cette belle propriété invariante du produit scalaire avec 4 points du plan (ou de l'espace): . Ici le consours des hauteurs devient "trivial": le point d'intersection de 2 hauteur appartient forcément à la 3ème hauteur. Un élève de 1^ère peut la démontrer (avec Chasles) en 2 lignes. Or on leur fait calculer des équations cartésiennes de hauteur, avec des coordonnées de points données, calculer leur point d'intersection. Mais aucune démonstration générale. C'est pénible et sans intérêt pour des élèves que je connais.

Mais revenons à nos moutons ...

Etant de la génération , règle à calcul et table de trigonométrie  , je ne suis pas concernée par tes remarques..
En partant de l'énoncé  donné  montrer que
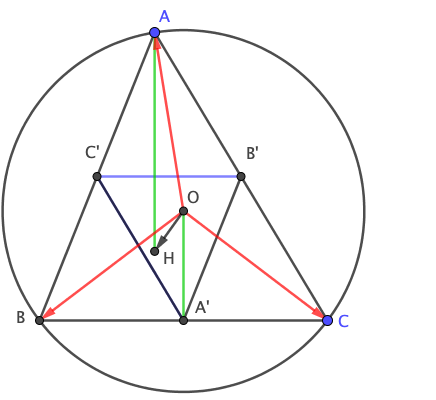
  A' milieu du segment [BC]  B' milieu du segment[AC] et C' milieu du segment  [AB]
Réciproque du Théorème de Thalès (niveau 4ème) permet de conclure que les triangles ABC et A'B'C' sont semblables  de coefficient    
Les médiatrices (OA')  ,(OB') et (OC')   respectivement des côtés [BC] ,[AC] et [AB]  sont  respectivement les hauteurs du triangle A'B'C' ( niveau  collège:si deux droites sont parallèles  ,toute droite  perpendiculaire à l'une est  perpendiculaire à l'autre)
  d'où  O est l' orthocentre de triangle  A'B' C'    or H est l'orthocentre  du triangle ABC    par suite ( les triangles sont semblables)  

A' milieu de [BC}
  

Merci PLSVU pour cette proposition. Mais trop classiquement liés aux milieux. Voici ce que j'ai finalement en tête ce matin, en évitant d'utiliser ces :

On a   et   orthogonaux à .
Donc leur somme l'est aussi, et par conséquent aussi.

idem pour (ou ), on arrive à orthogonal à ( ou )

2 relations suffisent pour dire que nécessairement . En effet, une droite ne peut pas être simultanément perpendiculaire à 2 droites sécantes.


Voilà. Avec du recul,  c'est propablement en connaissant déjà la relation qu'on a l'idée de faire la somme. Cette relation de Sylvester est un "coup de maître" qu'on ne peut qu'admirer.

Bonjourfabo34
J'ai le regret de te dire que c 'est inutile puisqu 'une seule égalité   du type  permet de  justifier l' égalité demandée
De plus l 'autre  expression  utilisée  est aussi justifiée par les milieux...

J'ai l'impression de parler à quelqu'un qui ne veut pas entendre.
Je répète: Je ne veux pas passer par les milieux!!!Et je veux faire le chemin inverse: pas démontrer l'égalité, mais y arriver!!

Je ne veux pas t'offenser. Donc ne sois pas aux regrets que je ne veuille pas utiliser ta démonstration. En maths il y a plusieurs outils. Toi veux utiliser le compas et la régle. Moi je préfère l'équerre. Je répète, le but est montrer aux élèves de 1^ère une façon "moderne" de considérer la géométrie. Ici avec le produit scalaire, qui est le condensé de plein de propriétés.  D'ailleurs, d'après sa biographie, Sylvester a travaillé sur la théorie des invariants. Et apparemment il existe "un groupe orthogonal pour lequel le produit scalaire est invariant". Bon, j'y comprends rien, mais je me dis que c'est probablement pour ça qu'on a donné le nom de la relation à ce mathématicien. Ou mieux, que c'est parce qu'il pensait en "invariant" que c'est le premier à avoir vu la relation entre O et H (?)

En te remerciant

Bonjour,
Sans parler des milieux
En partant  de ton calcul
  car