Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonctions trigonométriquesTopics traitant de Fonctions trigonométriques [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Points d'interdection

Posté par
oussema12 30-03-22 à 02:58

Bonsoir,

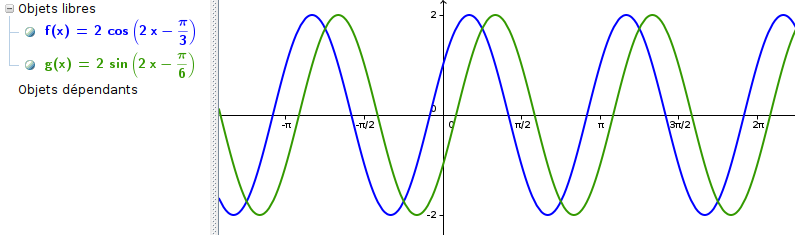
dans un exercice je dois trouvé les points d'intersection de Cf et Cg les courbes representatives respectivements de f et g
f et g definies sur R par
f(x) = 2cos(2x - \frac{\pi}{3})
g(x) =  2sin(2x - \frac{\pi}{6})
j'ai trouvé {Mk(/4 + k/2, 2cos(/6 + k)), k }
je veux eliminer le k dans les ordonnees des points alors j'ai fait

x = \frac{\pi}{4} + \frac{k\pi}{2}\: et\: y = 2cos(\frac{\pi}{6} + k\pi) \\ \Leftrightarrow x = \frac{\pi}{2} + k'\pi \: et \: y = 2cos(\frac{\pi}{6} + 2k'\pi) \: \\ ou \: x = \frac{3\pi}{4} + k'\pi \: et \: y = 2cos(\frac{\pi}{6} + \pi + 2k'\pi)
car k k' tel que k = 2k' ou k = 2k' + 1
(et je calcule pour trouver Ik, et Jk ayant respectivement 3 et -3 pour ordonnees)

la reponse est elle bien redigee comme cela
Merci d'avance

Posté par
malou Webmasterre : Points d'interdection 30-03-22 à 08:27

Bonjour

Points d\'interdection

et pourquoi ne pas travailler sur [0 ; [ et utiliser ensuite la périodicité de tes fonctions ? (car ton passage de la 1re à la 2e ligne n'est pas OK pour moi)


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !