Niveau Master

Problème de régression

Posté par
Togodumnus 08-03-16 à 09:33

Bonjour,

Je ne suis pas un grand amateur de statistiques, mais il faut s'y plier malheureusement.

En fait, je cherche à faire une régression suivant des probabilités qui dépendent d'un x et d'un t, que je vais noter $_tq_x$ .
Je bénéficie déjà de probabilités $_tq_x^{ref}$ qui vont constituer mes probabilités de référence.

Je cherche donc à avoir un modèle de régression entre les deux probabilités $_tq_x$ et $_tq_x^{ref}$

J'ai testé un premier modèle : $logit(_tq_x) = \theta_1 + \theta_2 logit(_tq_x^{ref})$ , donc avec $logit : x \mapsto \ln(\frac{x}{1-x})$

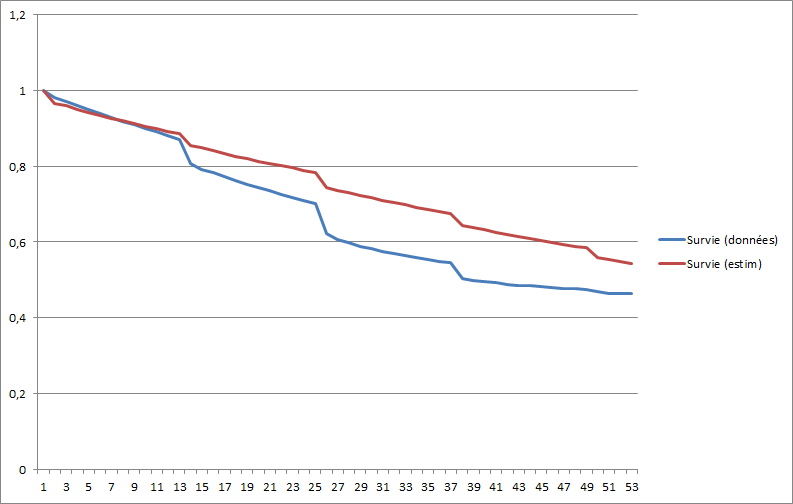
Problème de régression

Je trouve le modèle assez intéressant car les trois premières phases de la courbe sont relativement parallèles pour une simple modélisation. (Le temps aux abscisses est représenté en mois.)

Je comptais donc faire deux modélisations plus précises, mais qui ont l'inconvénient d'être plus difficiles à évaluer.

Modèle 1 : $logit(_tq_x) = logit(_tq_x^{ref}) + \theta_1 + \theta_2 E[\frac{t}{\textit{1 an}}]$ (E : fonction partie entière)
Ce modèle me permettrait de prendre en compte les "cassures" annuelles existantes tout en ne gardant que deux paramètres.

Modèle 2 : $logit(_tq_x) = logit(_tq_x^{ref}) + \theta_1 - \frac{\theta_2}{t} + \theta_3 \frac{t^2}{2} + \theta_4 \frac{\exp(\theta_5t)}{\theta_5}$
Ce modèle me permettrait de prendre en compte d'autres paramètres en considérant le cour terme (terme en 1/t), le moyen terme (terme en t^2) et le long terme (terme en exp).

Le seul problème, c'est que je ne vois absolument pas comment résoudre ces modèles.

Pour le premier modèle, j'ai eu l'idée d'utiliser le maximum de vraisemblance, mais le fait qu'il y ait une partie entière annihile totalement cette possibilité.

Pour le second modèle, j'ai pensé à utiliser le maximum de vraisemblance, notamment en utilisant la méthode de Newton. Mais ça me paraît extrêmement bourrin.
(Pour quelqu'un qui fait zéro maths, ça fait cinq dérivées partielles simples et vingt-cinq dérivées partielles doubles, sans compter les différentes erreurs possibles...)

Y aurait-il plus simple/efficace ?

Je vous remercie d'avance et vous souhaite une agréable journée.

Posté par re : Problème de régression 08-03-16 à 17:56

Bonjour,

J'ai pu avoir une réponse d'un prof, qui m'a dit que le modèle 2 n'avait pas été testé pour ce type de données.

J'ai donc choisi un remaniement de la méthode 1 :

$logit(_tq_x) = \theta_1 + \theta_2 logit(_tq_x^{\textit{ref}}) + \theta_3 (1_{t \ge 12} + 1_{t\ge 24})$ .

Pour ce faire, j'ai ajouté le troisième paramètre ( $\theta_3$ ) directement après avoir trouvé les deux premiers.

Ce troisième paramètre n'a aucun fondement théorique. En revanche, il me donne une excellente modélisation étant donné qu'il divise mon erreur quadratique par 44.

J'ai tout de même déterminé celui-ci par maximum de vraisemblance, mais ça m'a tout l'air d'être du bullshit. Néanmoins, je sais expliquer à quel phénomène correspond le choc.

Peut-être qu'une autre méthode d'estimation fonctionnerait mieux ?

Je vous remercie d'avance et vous souhaite une agréable soirée.

Posté par re : Problème de régression 08-03-16 à 21:22

Bonsoir Togodumnus.
Je crois que ton problème n'est pas un problème mathématique.

Si tu as un modèle, tu peux, en un sens, vérifier que ce modèle n'est pas à rejeter au vu des données et à un certain seuil de risque.

Mais, en rajoutant suffisamment de paramètres, on peut toujours avoir une coïncidence parfaite.

La question est alors : est-ce que les paramètres sont ad hoc, ou est ce qu'ils ont un sens. Et ce n'est pas une question mathématique.