Inscription / Connexion Nouveau Sujet
Probleme de Somme
bonjour,
J ai une complexité d'un programme a calculer et voici l expression que je trouve:
 (i0=1,n)
(i0=1,n)  (i1=1,i0) ...
(i1=1,i0) ...  (ik-1=1,ik-2)
(ik-1=1,ik-2)  (ik=1,ik-1) ik
(ik=1,ik-1) ik
J aimerai savoir si je peux faire majoré cette suite de somme?
J ai essayé mais sans succes  .
.
Merci
bon je vais vous dire comment j ai debuter,
 (i=1,n) i = (n+1)n/2, que j ai majoré a (n+1)²/2
(i=1,n) i = (n+1)n/2, que j ai majoré a (n+1)²/2
le probleme est de donner une majoration de :
 (i0=1,n)....
(i0=1,n).... (ik-1=1,ik-2)(ik-1+1)²/2
(ik-1=1,ik-2)(ik-1+1)²/2
La méthode qui a été donnée permet de calculer l'expression exacte de la somme S(n,k).
Si n ou k (ou tous deux) tend vers l'infini, S(n,k) tend vers l'infini. Il n'est donc pas possible de donner une borne supérieure. Mais on pourrait calculer un équivalent grâce à la formule de Stirling.
merci beaucoup, je sais pas comment j aurai trouver (j ai quelques lacunes en math et en info ca pardonne pas  )
)
Pourrais-tu me dire comment tu as trouvé :
S(n, k) = S(n-1, k) + S(n, k-1) ?
merci .
Ne vous inquiétez pas de ne pas avoir trouvé vous-même cette méthode, car c'était loin d'être évident et cela demandait un niveau assez élevé de pratique.

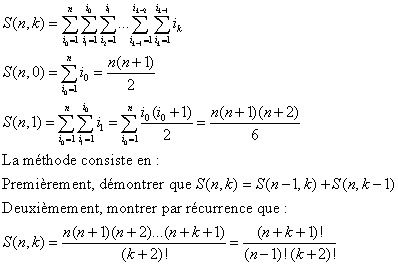
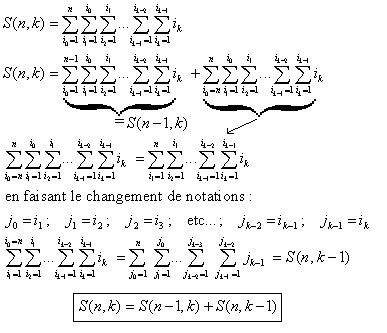

 analyse en post-bac
analyse en post-bac