Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

Problème. fonction f(x)= x² + x / | x² + x | +1

Posté par
toine 30-10-07 à 14:04

Je vous demande de l'aide pour mon probléme merci d'avance.

intitulé du problème :

soit f est la fonction numérique rèelle definie par f(x)= x² + x / | x² + x | +1 .

mon problème est composé de 9 question

1°/ Montrer que f est definie pour tout x rèel ?

2°/ f est elle continue sur ?

3°/ Exprimer f(x) sans le symbole de valeur absolue sur els intervalles convenables.

4°/ Etudier la derivabilité de f en x = -1

5°/ Etudier la derivabilité de f en x = 1

6°/ Calculer f'(x) aprés avoir précisé sur quels intervalles elle est derivable.

7°/ Calculer la lim x- f(x)
             la lim x f(x)

8°/ Etblir le tableau de variation de f en ecrivant la valeur exacte des réel qui interviennent dans le tableau

9°/ soit C la courbe représentaive de f dans un repére ( o, ) orthonormal ( unité 2 cm pour chaque axe )

a) C admet elle des asymptotes?

b) c admet elle des tangente horizonales ou des demi tangente ? ( si oui , préciser en quel point )

c) Preciser les coordonnées des point d'intersection de C avec l'axe des abscisses et la droite D d'quation y=1

d) construite C , ses asympotes eventuelles et les tangentes ou demi-tangente situées au b)



J'ai deja reflechi sur les question 1 à 8 , mais je ne suis pas sur de moi.   

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:13

Bonjour

Et quel est le fruit de tes réflexions ?

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:14

Au fait, tu n'as pas mis de parenthèses ; est-ce volontaire ?

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:16

tout mes escuse la fonction est (x²+x) / ( |x²-1| +1 )

on va prendre question par question.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:20

1°/ pour tout x , la valeur absolue de | x²-1 | est egale à

soit |x²-1| = -x²+1
soit |x²-16 = x²+1

d'ou f(x)= ( x²+x ) / (-x²+2 )
     f(x)= ( x²+x ) / x²  

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:25

Est-ce bien utile pour la question 1 ?

La fonction est définie ssi |x²-1|+1 est non nul ; cette condition est toujours vérifiée (une valeur absolue, "au pire" nulle, augmentée de 1 ne peut pas donner 0)

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:29

mais à propos quelle est la fonction (il y a une contradiction entre le titre et 14:16) ?

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:31

je me suis trompé dans le titre

la vrai fonction est f(x)= (x²+x) / ( |x²-1| +1 )

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:40

2°/ la fonction en valeur absolue est continue sur

f(x) = (x²+x) / ( |x²-1| +1 )

la fonction x x²+x est continue sur

la focntion x -x²+2 est continue sur

la focntion x x² est continue sur

donc la fonction f est continue sur

( je viens juste de le voir en cours alors je ne suis pas sur )

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:41

Un coup d'oeil graphique peut également être utile (ici avec "sinequanon", mais les calculettes font ça très bien aussi), sans que ce soit bien sûr une preuve.

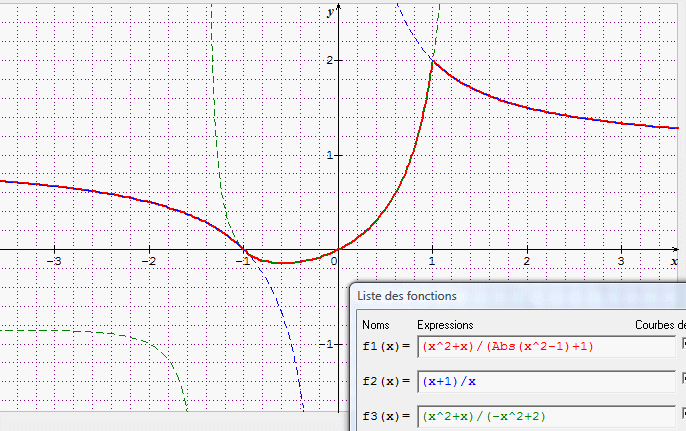
Problème. fonction f(x)= x² + x / | x² + x | +1

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 14:54

merci pour la représentation graphique.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:02

3°/

f(x)= (x²+x) / (-x²+2)

f(x)= (x+1) / x

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:03

Tu dois préciser sur quels intervalles tu te places.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:05

3°/

f(x)= (x²+x) / (-x²+2) sur

f(x)= (x+1) / x sur / {0}

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:08

Non

|x²-1| = x²-1 lorsque x²-1 0.

....

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:24

f1(x)= x² + x / | x² -1 | +1

3°/ f2(x)= x+1 / x sur car x0

f3(x)= x²+x / -x²+2

-x²+2 0
x² 2
x 2 ou x-2

Df3(x)= ] -; -2 [ U ] -2 ;2 [ U ] 2 ; + [

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:26

3°/

f2(x) est definie sur priver de 0

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:37

4°/ derivabilité en x=-1

lim x -1   x²+x / -x²+2 = -2/3

lim x -1   x²+x / x = 2

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:38

5°/ derivabilité en x=1

lim x -1   x²+x / -x²+2 = 2

lim x -1   x²+x / x = 2

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 15:48

Tu vas un peu vite en besogne. En particulier à la question 3 : ta réponse est fausse : relis mon post de 15:08

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 16:02

pourquoi x²-1 0. ??

et non -x²+2 0 !

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 16:12

Je n'ai pas écrit que x²-1 était positif, j'ai écrit : " |x²-1| = x²-1 lorsque x²-1 0 "

de même on a |x²-1| = -x²+1 lorsque x²-1 0

Donc deux cas à considérer :

d'une part x inférieur à -1 ou supérieur à 1
d'autre part x compris entre -1 et +1

...

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 16:47

oui c'est logique ! donc pour la question cette reponse conviens ?

1) j'ai la fonction f1(x)= x² + x / | x² - 1 | +1

definie dans un cas sur ] -; -1 [ U ] 1 ; + [
        dans l'autre cas sur ]-1 ; 1 [

2) la focntion f2(x)= x + 1 / x

definie sur privé de zero car x0

3) la focntion f3(x)= x²+x / -x²+2

definie sur ] -; -2 [ U ] -2 ;2 [ U ] 2 ; + [

car  -x²+2 0
     x² 2
     x - 2 ; x 2

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 16:58

non :

- 1er cas : x ]-;-1][1;+[

\tex f(x) = \frac{x^2+x}{(x^2-1)+1} = \frac{x^2+x}{x^2} = \frac{x+1}{x}

(aucun risque que x soit nul dans les intervalles considérés...)

- 2ème cas : x [-1;1]

\tex f(x) = \frac{x^2+x}{-(x^2-1)+1} = \frac{x^2+x}{-x^2+2}

(aucun risque que -x²+2 soit nul dans l'intervalle considéré ; d'autre part je ne vois pas pourquoi tu veux rendre à tout prix -x²+2 positif....)

et dans chaque question jette un oeil sur le graphique de 14:41 pour voir si le tout est cohérent.

...

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:11

je comprend , je ne prenais pas la fonction dans son ensemble mais en 2 sous fonction.

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:15

moi aussi

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:17

4°/ derivabilité en x=-1

lim x -1   x²+x / -x²+2 = -2/3

lim x -1   x²+1 / x = 0

5°/ derivabilité en x=1

lim x 1   x²+x / -x²+2 = 2

lim x 1   x²+1 / x = 2

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:25

Je ne comprends pas ce que tu fais ; on te demande d'étiudier la dérivabilité en -1 : quelle méthode utilises-tu et quelle est ta conclusion ?

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:34

j'utilise la formule

lim  x -1   f(x)-f(-1) / x+1

lim  x 1   f(x)-f(1) / x-1



la focntion f n'est pas derivable en x=-1 , mais elle est derivable a droite et a gauche de -1 et la courbe admet 2 demi-tangente de coefdirecteur -2/3 à gauche et 0 à droite

Mais cela ne me semble pas logique quand je regarde la courbe.

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:39

OK pour la méthode. Comment trouves-tu -2/3 et 0 ?

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:40

je vais refaire mes cacules j'ai du faire une erreur de signe.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 17:56

lim  x -1   f(x)-f(-1) / x+1

1er cas : [(x²+x)/x - (1²+1)+1] / x+1 = [x²+x)/x - 2 ]/ x+1

2er cas : [(x²+x)/-x²+2 - (1²+1)/-1²+2] / x+1 = [x²+x)/x - 2 ]/ x+1

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 18:03

D'abord remarque bien que f(-1) = 0.

Ensuite dans les deux cas tu pourras simplifier par x+1.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 18:20

4°/

1er cas

lim x -1 = (x²+x)/x * 1/x+1 = x²+x / x²+x = 1

2eme cas

lim x -1 = (x²+x)/-x²+2 * 1/x+1 = x²+x / -x²+2 * 1/x+1 = x²+x / -x^3-x²+2x+2

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 18:36

Je ne trouve pas ça :

- Lorsque x est strictement inférieur à -1 :

\Large \frac{f(x)-f(-1)}{x+1}=\frac{\frac{x+1}{x}}{x+1}=\frac{1}{x}

- Lorsque x est strictement supérieur à -1 :

\Large \frac{f(x)-f(-1)}{x+1}=\frac{\frac{x^2+x}{-x^2+2}}{x+1}=\frac{x}{-x^2+2}

sauf erreur et/ou faute(s) de frappe

Reste à trouver les limites à gauche et à droite du taux d'accroissement.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 30-10-07 à 18:47

d'accord.

on reprend demain.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 12:01

4°/ derivabilité en x = -1

lim  = (x²+x) /x /x+1 = 1 / x = 1 / -1 = -1
x -1
x < -1

lim  = (x²+x) /-x²+2 / x+1 = x / -x²+2 = 1/ -1²+2 = 1
x -1
x > -1

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 13:32

Non : tu dois étudier le comportement de

\frac{f(x)-f(1)}{x-1}

lorsque x tend vers 1 (même méthode que pour la dérivabilité de f en -1)

commence donc d'abord par calculer f(1).

....

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 13:40

f(1)=2 et f(-1)=0

pour la derivabilité en x=-1 la question 4 la formule est lim x -1 = f(x) - f(-1) / x+1

il faut voir 2 cas

lim  = (x²+x) /x /x+1 = 1 / x = 1 / -1 = -1
x -1
x < -1

lim  = (x²+x) /-x²+2 / x+1 = x / -x²+2 = 1/ -1²+2 = 1
x -1
x > -1

et pour la derivabilité en x= 1 question 5 la formule est lim x 1 = f(x) - f(1) / x-1

il faut voir 2 cas

lim  = [ (x²+x) / x ] -2 / x-1 = ...
x 1
x < 1

lim  = [ (x²+x) / -x²+2 ] - 2 / x-1 = ...
x 1
x > 1

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:09

Désolé, je croyais que tu avais fini la 4) et que tu étais à 5).

Fais attention aux parenthèses, ce n'est pas un détail.

Pour la dérivabilité en -1, ta limite à droite est fausse.

Pour la dérivabilité en 1, dans chaque cas, essaie d'arranger le numérateur et de faire sauter l'indétermination en factorisant par x-1.

...

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:14

im  = (x²+x) /-x²+2 / x+1 = x / -x²+2 = 1/ -1²+2 = 1
x -1
x > -1

cette limite est fausse ?

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:19

le numérateur est x ; si x tend vers -1, alors le numérateur tend vers -1 et pas vers 1.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:21

oui j'ai fait une erreur de signe !

question 5°/

lim  = [ (x²+x) / x ] -2 / x-1 = -(x-1)/x * 1/(x-1) = -1/x = -1
x 1
x < 1

mais je ne trouve pas la lim

lim  = [ (x²+x) / -x²+2 ] - 2 / x-1 = ...
x 1
x > 1

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:36

Pour l'erreur de signe, tu dois t'en rendre compte en observant le graphique d'hier
14:41 (même si je le répète ce n'est pas une preuve, c'est au moins un élément d'appréciation)

Pour la dérivabilité en 1, tu mélanges les deux : pour x proche de 1 par valeurs inférieures à 1 c'est f(x)=(x²+x)/(-x²+2).

Pou la limite manquante le numérateur d'écrit :

\Large \frac{x^2+x}{-x^2+2}-2=\frac{x^2+x-2(-x^2+2)}{-x^2+2}

tu l'arranges et tu essaies de factoriser par x-1 pour faire sauter l'indéternation liée au x-1 du dénominateur.
.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:46

je trouve -1 au 4 lim des 2 question 4°/ et 5°/

lim  = -1
x -1
x < -1

lim  = -1
x -1
x > -1


lim  = -1
x 1
x < 1

lim  = -1
x 1
x > 1

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:49

Ces résultats semblent-ils compatibles avec le graphique ?

Peux-tu détailler tes calculs pour la dérivabilité en 1 ?

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:53

question 5°/

lim  = ((x+1)/x)-2/(x-1) = (-x+1)/x /x-1 = -(x-1)/x * 1/x-1 = -1/x = -1/1 = -1
x 1
x < 1

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 14:55

lim  = x²+x-x²+2 / x-1 = x+2/x-1 = -2(x-1) - x / (x-1) = -x+1-x = -2x+1 = -1
x 1  
x > 1

Posté par
littleguyre : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 15:04

Je ne suis pas sûr que tu lises attentivement mes réponses.

Posté par
toinere : Problème. fonction f(x)= x² + x / | x² + x | +1 31-10-07 à 15:08

mes lim en 1 ne sont pas en concordance avec le graphique !

1 2 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !