Niveau autre

Problème pour étudier le sens de variation d'une fonction

Posté par
aygolf51 01-08-10 à 21:41

Bonsoir,

Je m'énerve sur un exercice c'est pourquoi j'ai besoin d'aide.
Voici l'exo:

On considère une fonction numérique f de la variable réelle x définie par :

f(x) = x^2 * ln|1-1/x |

1 Déterminer l'ensemble de définition Df de la fonction f.
2. Etudier la continuité et la dérivabilité de f sur son ensemble de définition.Calculer lorsqu'elle est définie , la dérivée de f.

3. Démontrer que f peut être prolongée par continuité en 0.Etudier la dérivabilité en 0 de ce prolongement, noté f barre.

4.Déterminer les variations de f barre sur Df U 0.Préciser les extrema locaux de f barre.

5 Etudier les limites de f barre aux bords de son ensemble de définition.

6. Démontrer que la courbe de f barre possède une asymptote verticale en 1 et une asymptote oblique en + ou - inf.

Je bloque sur la question 4.
J'espère que quelqu'un pourra m'aider parce que je ne vois pas comment faire.

Merci d'avance.

Posté par re : Problème pour étudier le sens de variation d'une fonction 02-08-10 à 00:54

Bonsoir,

Si $x<0$ ou $x>1$ , $f(x)=x^2\ln\,\left(1-\frac{1}{x}\right)$

$f'(x)=x\left[2\ln\,\left(1-\frac{1}{x}\right)+\frac{1}{x-1}\right]=xg(x)$

On étudie $g$ sur $]-\infty,0[\cup]1,+\infty[$

$g'(x)=\frac{x-2}{x(x-1)^2}$

Sur $]-\infty,0[$ , $g'(x)<0$ et $g$ est décroissante.

Sur $]1,2]$ , $g'(x)\leq 0$ et $g$ est décroissante.

Sur $[2,+\infty[$ , $g'(x)\geq 0$ et $g$ est croissante.

Une étude des limites pour $g$ en $-\infty$ et $0^-$ permet d' affirmer que $g(x)>0$ sur $]-\infty,0[$

Sur l' intervalle $]1,+\infty[$ , on a $g(2)=1-2\ln\,2<0$ , $\lim_{x\to 1^+}g(x)=+\infty$ et $\lim_{x\to +\infty}g(x)=+\infty$

Le théorème des valeurs intermédiaires sur $]1,2]$ permet d' affirmer que $g(x)$ s' annulle en un unique $\alpha \in ]1,2]$

En résumé:

sur $]-\infty,0[$ , $g(x)>0$ et $f'(x)=xg(x)<0$ donc $f$ est décroissante

sur $]1,\alpha]$ , $g(x)\geq 0$ et $f'(x)=xg(x)\geq 0$ donc $f$ est croissante

sur $[\alpha, +\infty[$ , $g(x)\leq 0$ et $f'(x)=xg(x)<0$ donc $f$ est décroissante.

Reste à étudier de la même manière ce qui se passe sur $]0,1[$ avec $f(x)=x^2\ln\,\left(\frac{1}{x}-1\right)$

On aura $f'(x)=x\left[2\ln\,\left(\frac{1}{x}\right)+\frac{1}{x+1}\right]=xh(x)$

En principe tu prouveras l' existence d' un réel $\beta\in ]0,1[$ tel que $h(\beta)=0$ :

sur $]0,\beta]$ $f'(x)\geq 0$ et $f$ est croissante.

sur $[\beta ,1[$ , $f'(x)\leq 0$ et $f$ est décroissante.

$\alpha \approx 1.40$ et $\beta\approx 0.32$

Voici la courbe:

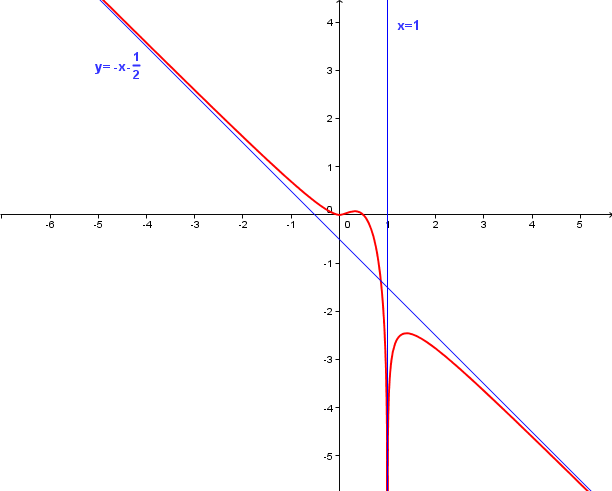
$Problème pour étudier le sens de variation d\'une fonction$

Posté par re : Problème pour étudier le sens de variation d'une fonction 02-08-10 à 08:22

bonjour,
>>cailloux
il me semble que tu as mal recopié ton expression de h(x) (ou je suis mal réveillée)

Posté par

02-08-10 à 09:15

Merci beaucoup cailloux!! Je vais regarder ça attentivement.
En plus quelle rapidité!! Merci encore!
J'avais posé une fonction g mais pas celle ci.

Posté par re : Problème pour étudier le sens de variation d'une fonction 02-08-10 à 10:25

Pour le moment, je ne trouve la même chose à part que pour moi la fonction g est croissante sur ]-, 0[.

Posté par re : Problème pour étudier le sens de variation d'une fonction 02-08-10 à 11:11

Bonjour à tous,

Oui veleda, tu as raison:

Sur $]0,1[$ , $h(x)=2\,\ln\left(\frac{1}{x}-1\right)+\frac{1}{x-1}$

Citation :
à part que pour moi la fonction g est croissante sur ]-

, 0[.

tu as aussi raison: une erreur de recopiage...

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

analyse en post-bac
24 fiches de mathématiques sur "analyse" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Problème pour étudier le sens de variation d'une fonction

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths