Bonjour laure

Ton texte n'est pas très clair : tu dis que I et J sont les milieux respectifs des côtés [AB] et [AC]... mais [AC] n'est pas un côté du carré ABCD non ?

Plus loin tu écris : vecteur DJ=1/2 de vecteur BC, ce que je traduis par ...

Avant de continuer, pourrais-tu confirmer que la figure ci-dessous correspond à ton énoncé et qu'il s'agit bien de montrer que :

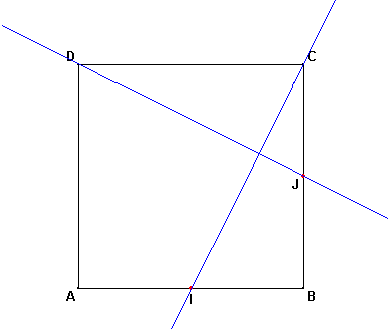
1 "des côtés [AB],[AC]"
AC n'est pas un côté du carré
J doit être le milieu de BC

de plus "vecteur DJ=1/2 de vecteur BC et vecteur CI=1/2 de vecteur AB"

NON seuls les vecteurs colinéaires peuvent faire l'objet d'une relation :
vect AB = k*vect XY

2 En calcul vectoriel il faut décomposer les vecteurs. Le mieux est de choisir un repère. ici les vecteurs AB et AD

3 On va calculer le produit scalaire DJ.CI

en vecteur DJ=DA+AJ=DA+AB+BJ
or BJ=AD/2 soit DJ= AB-AD/2

CI=CB+BI or CB=-AD et BI=-AB/2 soit CI=-AD-AB/2

DJ.CI=(AB-AD/2).(-AD-AB/2)=(-AB.AD+1/2*AD^2-1/2*AB^2+1/4*AB.AD)=0
car AD^2=AB^2