Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
produit scalaire
Posté par marypohl
bonjour je voudrais de laide pour un exo
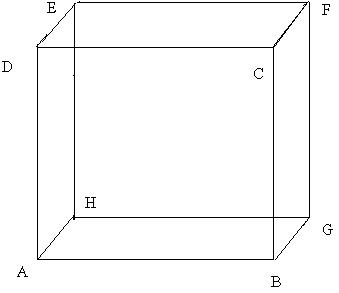
c'est un cube
on etudie dabord la face EHGF
I est le milieu de GH
P est le point d'intersection de (EG) et (FI)
il faut montrer que P est le centre de gravité du triangle FGH
moi je sais donc qu'il faut montrer que 3FP=2FI
mai je n'arive pas à le faire
sur la face du haut
et je sais que le centre de gravité est le point de rencontre des médianes, c'es pourquoi je dit qu'il faut surment trouver que 3 FP= 2FI
Posté par BiG-CaT (invité)oki
Par definition , FI est une mediane du triangle FGH.
Il faut prouver que OG est une mediane du trinagle FGH
O est le point de rencontre des diagonales => O milieu de FH , donc OG mediane du triangle FGH.
Point de rencontre de 2 mediane => centre de gravité
Bonjour,
soit le barycentre de
barycentre de
où
est le milieu de
par associativité et
Mais est aussi le barycentre de
toujours par associativité. Donc
et
je dois aussi montrer que Q est le centre de gravité de FBG
Q point d'intersection de FC et GJ
avec J milieu de FB
je l'ai fai ac le barycentre
Soit N le barycentre de (B,1),(F,1),(G,1)
J étant le milieu de BF donc J barycentre de (G,1) (F,1)
docn N barycentre de (G,1),(J,2)
par association N appartient à JG
Soit R milieu de BG, N est le barycentre de (F,1),(R,2)
par association N appartient à FR avec R milieu de FC
donc N appartient à FC et JG
docn N=Q et Q est donc le centre de gravité du triangle FBG
c'est bon?