- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour,
Je suis complètement bloquée sur l'exercice suivant :
Dans un repère orthonormal (o ; i ; j ; k) de l'espace, on considère la sphère S de centre A(2 ; -3 ; 1) et de rayon 2 et le plan P d'équation 3x - 6y + 2z = 0
1/ Calculer la distance du point A au plan P et en déduire que S et P n'ont pas de points communs.
J'ai fait
 = (|2*3 + (-3)*(-6) + 1*2|)/(
= (|2*3 + (-3)*(-6) + 1*2|)/( (3² + (-6)² + 2²)) = 26/
(3² + (-6)² + 2²)) = 26/ 47 mais ne sais pas en déduire que S et P n'ont pas de points communs. Est-ce exact ce que j'ai fait ?
47 mais ne sais pas en déduire que S et P n'ont pas de points communs. Est-ce exact ce que j'ai fait ?
2/ Soit B le point de la sphère S dont la distance du plan P est la plus courte. Quelle est la distance du point B au plan P.
Je ne sais pas quoi faire vu que je ne peux pas le faire avec les coordonnées de B (que je ne crois pas pouvoir avoir de tout façon) que je dois déduire à la question 4.
3/ Déterminer les coordonnées des vecteurs n et n' orthogonaux au plan P et de norme 2
J'avais pensé à :
vecteur n (3 ; -6 ; 2) mais je ne saurais dire pour un deuxième vecteur...
Je sais aussi que ||vecteur n|| = 2 et ||vecteur n|| =  (a² + b² + c²)
(a² + b² + c²)
Donc 2² = a² + b² + c² mais que faire avec ça ? Est-ce que ça me sert d'ailleurs ?
4/ Déduire les coordonnées du point B
Merci d'avance pour vos réponses 
kaczka 
Erreur de calcul, mais soit:
d = (|2*3 + (-3)*(-6) + 1*2|)/V((3² + (-6)² + 2²)) = 26/V49 = 26/7
On a donc d > 2.
La distance du plan au centre de la sphère est supérieure au rayon de la sphère --> la sphère et le plan n'ont pas de point commun.

Ah merci ! Pas bien compliqué en fait, je cherchais à faire des tonnes de calculs !
Et puis me disais aussi pour ce 26/ 47... Il ne plaisait pas beaucoup !
47... Il ne plaisait pas beaucoup !
Merci, kaczka 
Ne pense pas tout sous forme de formule.
Réfléchis et la réponse sera alors souvent évidente, comme ci-dessous:
2)
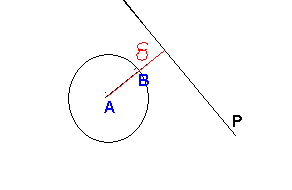
La distance du point B au plan P est égal à [tex]delta - R = 26/7 - 2 = 12/7
-----
Sauf distraction. 
Ah ouais... Je cherche toujours la réponse claire et précise dans le cours 
Bon en tout cas merci beaucoup 
3)
un vecteur orthogonal au plan P est (3 ; -6 ; 2), sa norme est V(3²+6²+2²) = V49 = 7
--> le vecteur (2/7) * (3 ; -6 ; 2), soit de coordonnées (6/7 ; -12/7 ; 4/7) est orthogonal P et de norme 2.
Le vecteur de même, norme, de même direction et de sens contraire convient aussi.
On a donc :
vecteur n  6/7 ; -12/7 ; 4/7)
6/7 ; -12/7 ; 4/7)
vecteur n'  -6/7 ; 12/7 ; -4/7)
-6/7 ; 12/7 ; -4/7)
-----
4)
Avec B'(X;Y;Z), on a :
vecteur n = vecteur (AB') :
(6/7 ; -12/7 ; 4/7) = (X - 2 ; Y + 3 ; Z - 1)
X = 20/7 ; Y = -33/7 ; Z = 11/7
--> B'(20/7 ; -33/7 ; 11/7)
Avec B''(X;Y;Z), on a :
vecteur n' = vecteur (AB) :
(-6/7 ; 12/7 ; -4/7) = (X - 2 ; Y + 3 ; Z - 1)
X = 8/7 ; Y = -9/7 ; Z = 3/7
--> B''(8/7 ; -9/7 ; 3/7)
B est soit le point B', soit le point B''
Distance du point B' au plan P: |(3*20/7 - 6*(-33/7) + 2*11/7 )/V(3² + 6² + 2²)| = 280/49 = 40/7
Distance du point B'' au plan P: |(3*8/7 - 6*(-9/7) + 2*3/7 )/V(3² + 6² + 2²)| = 84/47 = 12/7
Et donc B est le point B''
--> B(8/7 ; -9/7 ; 3/7)
-----
Sauf distraction. 


