bonjour,

une petite figure pour être sure que les points sont au bon endroit et qui laisse aussi pressentir le resultat de la derniere question .



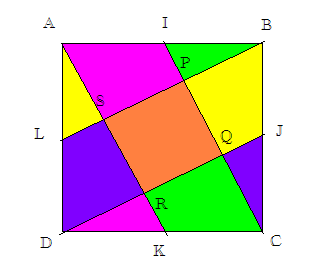
2) en vecteurs:
IC.BL = (IB+BC) .(BC+CD+DL)
= IB.BC + IB.CD + IB.DL + BC² + BC.CD + BC.DL
= 0 - a²/2 + 0 + a² + 0 - a²/2
= 0

le quadrilatere possede donc un angle droit.

6)a) en vecteurs:
BA.BL = BA² ( L se projette en A sur (AB))
= a²

IA.BL = (1/2 BA).BL
= (1/2) BA.BL
= a²/2

b) en vecteurs:
IA .BL = (BA-BI).BL
= BA.BL - BI.BL
= BS.BL - BP.BL ( methode du projeté)
= (BS-BP).BL
= SP.BL

et la meme chose en longueurs puisque colineaires.

c) Pythagore dans ABL donne BL = a
donc

a²/2 = PS. a d'où PS =a

7) je suppose que c'est la methode de la question 6 dont tu veux parler. Je te laisse faire sur le meme modele.

8)PQRS est donc un carré
fais le rapport des longueurs.
les aires ont le meme rapport au carré.

tu trouveras aire PQRS = aire ABCD ce que te montrent les couleurs sur le dessin.

Bonjour et merci

Sur le schéma qui est donné dans l'exercice le point A est en bas à gauche, le point B est en bas à droite, le point C en haut à droite...

Donc dans le petit carré R est en haut et S à gauche et P en bas

Voila !!

Merci

Ça n'a pas d'importance dans la mesure où tout le reste coïncide.
J'ai fait attention que PQRS soient correctement placés pour que les hypothèses soient vérifiées.

Bonjour,

Comment justifier rigoureusement que PQRS est un parallélogramme ?

Merci d'avance

Puis pour la question 3) b)

Comment démontrer que c'est colinéaire ??

bonjour,

pour 3b) P et S sont les points d'intersection de (BL) avec deux autres droites , donc forcement sur le droite (BL) d'où la colinearité.

pour le parallelogramme PQRS , tu peux par exemple utiliser la translation de vecteur
L --> D
B --> J donc (BL) //(DJ)

meme chose à l'horizontale , dans la translation de vecteur
A --> I
K --> C donc (AK)//(IC)

deux paralleles qui coupent deux autres paralleles forment un parallelo à leur intersection.

D"accord

Pour la question 4, je dois partir de (vecteur) BC.BI ?

( y a pas de question 4 )

non il faut partir de

en deduire

montrer que

en deduire

^^" La question 7 ...

Merci beaucoup

de rien !

Pour la question 4 ,

CB.CI = CB² = a²

J'en déduis JB.CI = (1/2 .CB) . CI
                  = (1/2) .CB.CI
                  = a²/2

Je démontre que

JB.CI  = (BC-BJ).CI = BC.CI - BJ.CI = (puis il faut projecté C et J) = BP.CI - BQ.CI = (BP-BQ).CI = PQ.CI

JB.CI = QP.CI

Idem pour les longueurs car coliénaires ?


Et je bloque pour Pythagore  (il faut trouver comme dans la question 3) c) ?)

Merci ...

oui les points IPQC sont alignes dans ce sens et donc le produit scalaire vaut le produit des normes.

pour Pythagore dans BIC rectangle en B tu trouves

Ok donc

(vecteur) JB.CI = PQ.CI = (longueur) PQ.CI

BC² + BI² = CI²
a² + [(1/2)a]²= CI²

...

Est ce que c'est ca ?

voui !

a²/2 = PQ.[(racine)5/ 2] a  d'où PQ = [(racine)5/2] a

non

Ah oui comme pour PS

Merci !!

Bon bein voila ... J'ai fini de rédiger cet exercice

Il me reste plus que celui : https://www.ilemaths.net/sujet-second-degres-260601.html


Merci pour votre aide !!

de rien!
_{je dois quitter l'ile , je repasserai peut être voir ton deuxieme sujet ce soir , si personne n'a encore repondu !}

Ce serait avec plaisir