Salut tout le monde!
J'ai un problème avec un exercice sur le produit scalaire et sur la géométrie dans l'espace. Voici l'exo :
Enoncé :
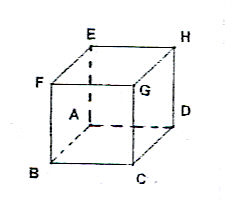
AB=a, ABCDEFGH est un cube, A se projette orthogonalement en K sur (FD)
                            G se projette orthogonalement en L sur (FD)
Questions :
1) Montrer que B et E se projettent orthogonalement en L sur (FD)
2) Montrer que C et H se projettent orthogonalement en K sur (FD)
3) Vérifier que \vec{FE}=\vec{BA}=\vec{CD}. En déduire \vec{FL}=\vec{LK}=\vec{KD} , en déduire FL


Voilà je sais qu'il faut utiliser le produit scalaire alors j'ai utilisé le repère orthonormal (A;B;D;E)
Puis j'ai cherché les coordonnées de tous les points :
A(0;0;0)
B(a;0;0)
D(0;a;0)
E(0;0;a)
F(a;0;a)
H(0;a;a)
C(a;a;0)
G(a;a;a)
Je sais que pour prouver que deux vecteurs sont orthogonal, il faut prouver que leur produit scalaire est égal à 0 mais après je sais pas trop comment faire
J'ai aussi une question qui n'est pas niveau terminale mais plus 4ème : les diagonales d'un cube sont-elles orthogonales et se coupent-elles en leur milieux? Si oui alors les points K et L sont logiquement confondus non?


Merci d'avance pour votre aide!

P.S: je suis nouveau sur le forum!