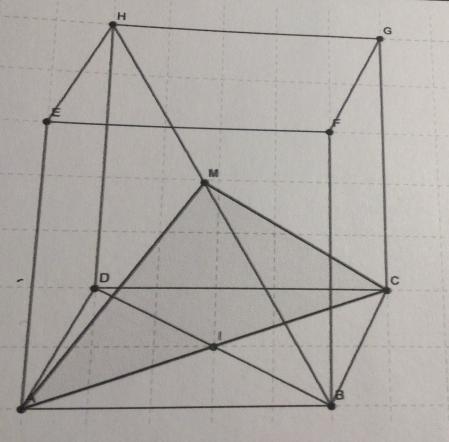
La figure ci dessus est un cube , l'unité de longueur est l'arrête du cube. Un point M mobile de déplacé sur la «grande» diagonale  [HB] du cube.
Le but de l'exercice est de déterminer la position Mo du point L sur ke segment [HB] pour laquelle l'air du triangle AMC est minimale.

1- Calculer l'air des triangles ABC et AHC
2- Montrer que le plan médiateur de [AC] est le plan (DBFH)
3- Montrer que le triangle AMC est isocèle et que l'air (AMC)= (AC.MI)/2 ou I est le milieu de [AC]

4- Solution analytique , on choisit le repère orthonormé ( D,DA,DC,DH)

a) montrer qu'un point M(x,y,z) appartient à [HB] si et seulement si il existe t appartient [0,1] tel que x=t, y=1 et z=1-t

b) Montrer que quelque soit t appartient à [0,1] , l'air AMC = 2/2 * 3t**2 -4t +3/2
Étudier le sens de variation de la fonction f définie sur [0,1] par f(t)= aire (AMC) puis conclure .

c) Déterminer  les coordonne du point Mo puis montrer que les points I,Mo et F sith alignés

5- Solution géométrique

a) représenter le rectangle HDBF en respectant les proportions puis déterminer et construire le point Mo tel que la distance MI soit minimale

b) Calculer IF.BH sans utiliser de repère , en déduire que les points I.Mo et F sont aligné