- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Produit scalaire cube
Bonsoir,
je bloque depuis hier sur le scalaire AJ.BH, je ne comprends pas très bien quelle relation de Chasles on doit utiliser (si tant est qu'on doive l'utiliser!)
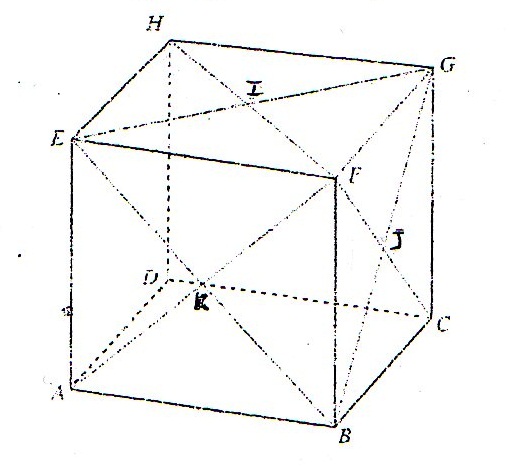
Le cube ci-dessous a pour arête a.
Merci de votre aide
Bonjour,
Décompose chacun des vecteurs en 3 sous vecteurs composant les arrêtes du cube (par exemple AJ se décompose en AB,(1/2)BC et (1/2)BF), ensuite développes. Plusieurs termes orthogonaux vont disparaitre, le reste devrait être assez simple à calculer.
Je comprends pas ton expemple.
Tu dis que AJ=AB=(1/2)BC=(1/2)BF? Ou ce sont des +?
Je vois pas le rapport, je ne vois pas Chasles là dedans?
Ah d'accord... Merci.
J'ai essayé de décomposer après avoir établi la relation suivante:
.
=(
+
).(
+
)
= .
+
.
+
^2+
.
C'est le seul vecteur dont on n'a pas de valeur maintenant. J'ai fait ça, mais je ne suis pas sur que ce soit ça:
=
+
+
=+
+
=(
+
)+
+
Ca parait bizarre non?
En effet, c'est bizarre. En fait l'idée est d'exprimer chaque vecteur en fonction des arêtes du cube, une fois fait, les produits scalaire ne seront plus que deux cas possibles : soit les vecteurs sont orthogonaux, et le produit scalaire est nul, soit les vecteurs sont égaux et le produit scalaire est égale à la longueur d'une arête au carré.
(simplement Chasles)
Sur ces neufs produits scalaires, 6 sont nuls et 3 s'exprime comme une fraction de + ou moins a² (a étant le côté du cube)
Et si je ne me trompe pas on trouve en définitive -a²+(1/2)a²+(1/2)a² = 0, ce qui signifie que les vecteurs sont orthogonaux. Je te laisse, je dois m'absenter, si tu ne comprends toujours pas j'espère qu'une âme charitable passera par là.
Du coup je vois pas le rapport avec le développement de ou
que tu m'avais proposé initialement?
Mais sinon j'ai bien compris tôn dernier calcul, je tombe sur , juste?


