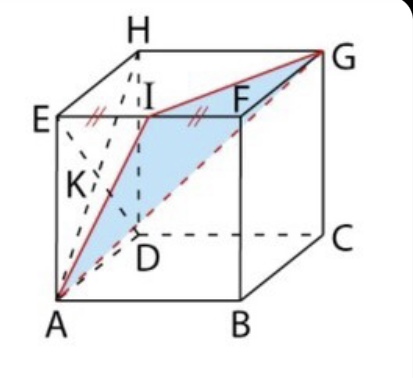
salut

pourtant on te mâche tout le travail dans chaque question !!

quelle relation lie les vecteurs AK et BG ?

Les deux vecteurs sont parallèle

ça ne veut rien dire ... (revoir un cours de seconde ou première) ...

des droites sont parallèles ... (ou pas) ...

Ducoup j'ai essayer de faire quelque chose mais je ne sait pas si je peut aboutir a quelque chose avec sa :
Je sait que BK=BA+AK et que AG=AB+BG
hors AK=1/2AE+1/2AD et BG=BF+FG
Alors :
BK.AG=(BA+1/2AE+1/2AD)(AB+BF+FG)
Je développe :
BK.AG=BA.AB+BA.BF+BA.FG+1/2AE.AB+1/2AE.BF+1/2AE.FG+1/2AD.AB+1/2AD.BF+1/2AD.FG
Si je réduit j'ai :
BK.AG=BA.AB+1/2AE.BF+1/2AD.FG
Et la je bloque je ne sait pas comment réduire ceci

Et non du coup si les droites sont parallèles les vecteurs sont colinéaires

ok mais on peut dire encore mieux : qui dit vecteurs colinéaires dit coefficient de colinéarité !! et quel est-il ici ?

on peut alors réduire considérablement tes calculs ...

Bien AK=1/2BG

et bien voila !!

donc tu peux te simplifier considérablement les calculs ...

Ok donc Je sait que BK=BA+AK et que AG=AB+BG
hors AK=1/2BG et BG=BF+FG
Alors : BK.AG=(BA+1/2BG)(AB+BF+FG)
Je distribue :
Bk.AG=BA.AB+BA.BF+BA.FG+1/2BG.AB+ 1/2BG.BF+1/2BG.FG
Je simplifie :
BK.AG=BA.AB+1/2BG.AB+1/2BG.BF+
1/2BG.FG  sauf que la je bloque je ne sait pas comment aller plus loin

inutile de décomposer BG ...

et repère les vecteurs égaux dans le cube ...

Ok donc sa fait que:
Je sait que BK=BA+AK et AG=AB+BG
Hors AK=1/2BG donc BK=BA+1/2BG
Donc j'ai:
BK.AG=(BA+1/2BG)(AB+BG)
BK.AG=BA.AB+BA.BG+1/2BG.AB+
1/2BG.BG
Sauf que la je ne sait pas comment réduire
Et sinon les vecteurs égaux sont
AB=EF=HG=DC
AD=EH=FG=BC
AH=BG
AF=DG
EG=AC
HF=DB
EB=HC
ED=FC

ok c'est tout bon ...

Ah oui mais je comprend pas quelque chose on ne peut pas réduire la si?
Enfin j'ai BK.AG=BA.AB+BA.BG+1/2BG.AB+
1/2BG.BG
je peut dire
BK.AG=-AB²+BA.BG+1/2BG.AB+
1/2BG.BG  mais je ne sait pas comment réduire plus

Ouai je suis d'accord mais il y en as beaucoup trop je vais pas les écrire je sait que AB et BF sont orthogonaux par exemple mais pour reduire cela ne me sert a rien par exemple l'ange ABG ne fait pas 90° donc ce n'est pas orthogonal

J'ai rien dit j'suis un petit peut long a comprendre oui effectivement BA et BG sont orthogonaux donc valent 0 et 1/2BG.AB sont orthogonaux aussi se qui fait qu'il me reste
BK.AG=-AB²+ 1/2BG.BG

ben ne regarde que ce qui apparaissent dans ton résultat final !!!

Oui desolé je me suis corriger au dessus il ne reste donc que
BK.AG=-AB²+ 1/2BG.BG

Par contre j'ai beau réfléchir je ne comprend pas comment réduire 1/2BG.BG a moin que cela ne fasse que 1/2BG en fin de compte je ne suis pas sur

un peu de sérieux !! : BG * BG = BG

diagonale d'un carré ...

Oui mais on as 1/2 devant BG et 0,5x1=0,5 donc 1/2BG.BG= BG non je ne comprend pas bien

Ah non je suis pas sur mais ducoup on aurais
BK.AG=-AB²+ (BG²/2)

ne sais-tu pas calculer la diagonale d'un carré ? (collège)

Beh BC²+CG²=BG²

Mais je ne comprend pas a quoi cela peut me mener avec mon 1/2BG.BG il faut que je remplace par((BC²+CG²)/2).(BC²+CG²) ?

J'ai pas bien compris le coté du cube? Celui concerné par BG? C'est BCGF?
Mais du coup nous en étions a
BK.AG=-AB²+ 1/2BG.BG
Or on as dit que BG² c'est BC²+CG² donc on as
BK.AG=-AB²+((BC²+CG²)/2).(BC²+CG²) mais ducoup si je ne met pas les racines les carrés disparaissent? Faut il que je distribue mes parenthèses maintenant?

Bonjour,

Je me permets d'apporter un petit coup de main à Nearraa.

En fait tu as BG²=BC²+CG² = 2 * AB² (car dans un cube toutes les arrêtes sont égales)
Et donc BG = = AB

En fait, la longueur de la diagonale d'un carré est toujours égale à multiplié par la longueur du côté du carré.

euh j'ai pas bien compris la?
sa veut dire que j'ai BK.AG=-AB²+((2xAB²) ?
j'ai pas bien compris

Bonjour,
16h43 : BK.AG = - AB² + 1/2 BG.BG .
Ensuite :
BK.AG = - AB² + 1/2 BG² = - AB² + 1/2(2BC²) .
Et si tu appelles  a  la longueur des côtés du cube . . . .

Ah ok je crois que je l'ai sa me fait 1/2(2AB²) donc on as donc -AB²+AB² donc le produit scalaire vaut 0

D'accord.

C'est ça?

Oui. Tu peux maintenant attaquer la question 1.b).

Pour la 1)b)
Je sait que BK=BA+AK et que AI=AE+EI or AK=1/2BG et EI=1/2EF
J'ai:
BK.AI=(BA+1/2BG).(AE+1/2EF)
BK.AI=BA.AE+BA.1/2EF+1/2BG.AE+
1/2BG.1/2EF
Soit BK.AI=BA.1/2EF+1/2BG.AE
Par contre de la je ne sait plus d'où m'orienter

Maintenant, remplace EF par AB et BG par BF + FG.

En gros j'aurais
BK.AI=-AB.AB+(1/2(BF+FG)).AE
Donc:
BK.AI=-AB²+(1/2(BF+FG)).AE
Je distribue le BF et FG sur AE?

FG.AE = ??

FG.AE=0 c'est orthogonal

Ducoup il reste
BK.AI=-AB²+1/2(BF.AE)
Sauff que BF et AE sont égaux donc cela revient a BF.BF donc
BK.AI=-AB²+1/2(BF²)
Or c'est un carrée et chaque arrête est égal donc BF=AB  donc on as
BK.AI=-AB²+1/2(AB²)
Seul détail le 1/2 me bloque

Le premier terme de l'expression de BK.AI est erroné (cf 18h22 et 19h58).

Je comprend pas il fallais laisser AK et pas 1/2BG?

Le premier terme est  - 1/2 AB²  et non  - AB² .

Je comprend pas a partir d'ou est l'erreur
J'ai BK.AI=(BA+1/2BG).(AE+1/2EF)  si je distribue je reviens a ce que j'ai fait dans l'énoncé on me dit que BK c'est BA+AK mais AK c'est 1/2BG je comprend pas

Ah oui pardon je recommence
Je sait que BK=BA+AK et que AI=AE+EI or AK=1/2BG et EI=1/2EF
J'ai:
BK.AI=(BA+1/2BG).(AE+1/2EF)
BK.AI=BA.AE+BA.1/2EF+1/2BG.AE+
1/2BG.1/2EF
Soit BK.AI=BA.1/2EF+1/2BG.AE
Maintenant je remplace EF par AB donc j'ai:
BK.AI=-AB.1/2AB+1/2BG.AE
Maintenant je remplace BG par BF + FG.
BK.AI=-AB.1/2AB+(1/2(BF+FG).AE
Je distribue:
BK.AI=-AB.1/2AB+(1/2(BF.AE+FG.AE)
Or FG.AE=0 donc il me reste
BK.AI=-AB.1/2AB+(1/2(BF.AE)
Or BF et AE sont égaux donc j'ai  
BK.AI=-AB.1/2AB+(1/2(BF²)
Mais nous sommes dans un carrée chaque arête est égale je peut donc remplacer BF par AB donc:
BK.AI=-AB.1/2AB+(1/2(AB²)
Soit -1/2 AB² + 1/2 AB² = 0
Donc BK.AI=0 c'est ça?

Oui.

Pour la 1)c) il me suffit de dire que étant donné que BK est orthogonal a AG et que BK et aussi orthogonal a AI par conséquent je peut dire que BK est orthogonal au plan (AIG) c'est ça?

Oui.