Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
produit scalaire dans l'espace
Posté par Marie-C
Bonjour
Voilà, j'ai un DM à faire et quelques questions à partir de la partie B, 2) me posent problème.Je vous mets l'énoncé en entier pour que vous disposiez de toutes les informations
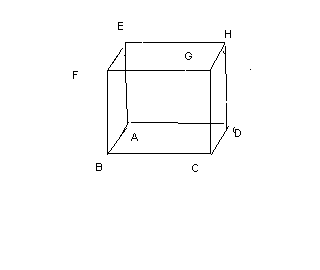
ABCDEFGH est le cube d'arête 1. L'espace est rapporté au repère orthonormal (A,
Partie A
1) démontrer que le triangle BDE est équilatéral
2) I: centre de gravité du triangle BDE
a) calcul des coordonnées de
b) démontrer que
3) Prouver que I est le projeté orthogonal de A sur le plan (BDE)
Partie B:Pour tout réel k, on définit deux points Mket Nk, ainsi qu'un plan Pkde la façon suivante
Mk: point de la droite (AG) tel que
Pk: plan passant par Mk et parallèle au plan (BDE)
Nk: point d'intersection du plan Pk et de la droite (BC)
2)
a) calculer les coordonnées de Mk dans le repère (A,
b) déterminer une équation du plan Pk dans ce repère
c) en déduire que le point Nk a pour coordonées (1,3k-1,0)
3) Pour quelles valeurs de K la droite (MkNk) est elle orthogonale à la fois aux droites (AG) et (BC)
donc 0k=0 bizarre 
4) Pour quelles valeurs de k, la distance MkNk est elle minimale?
merci d'avance
Bonjour Marie-C, 
La partie B suit la partie A...
Dans la partie A
. tu as montré que l'intersection du plan (BDE) et de (AG) est en I : (1/3 ; 1/3 ; 1/3)
. et tu sais que le plan (BDE) coupe les axes en trois points (1 ; 0 ; 0), (0 ; 1 ; 0) et (0 ; 0 ;1)
Tu peux trouver sans mal que l'équation du plan (BDE) est
(x/1) + (y/1) + (z/1) = 1
Dans la partie B
homothétie de rapport 3k puisque
Donc : d'accord pour les coordonnées de M : (k ; k ; k)
Le plan Pk coupe maintenant les axes aux points (3k ; 0 ; 0), (0 ; 3k ; 0) et (0 ; 0 ; 3k)
donc son équation est
(x/3k) + (y/3k) + (z/3k) = 1
Dans le plan de base ABCD, l'équation de l'intersection du plan Pk est y = 3k - x
donc les coordonnées du point Nk sont (1 ; 3k-1 ; 0)
Je te laisse continuer
A retenir absolument (surtout si un jour tu fais de la cristallographie) :
le plan dont les intersections avec les axes sont les points de coordonnées (a ; 0 ; 0), (0 ; b ; 0) et (0 ; 0 ; c)
a pour équation :
(x/a) + (y/b) + (z/c) = 1
Merci Coll de ta réponse
C'est quoi la cristallographie??
Pour la question 3
C'est bon, ce que j'ai mis?
donc on a (1-k)+(3k-1-k)+(0-k)=0
0k= 0 c'est bizarre
avec BC (0,1,0)
donc (2k-1)= 0
merci
La cristallographie : l'étude des cristaux
Tu sais que les "pierres précieuses" sont taillées pour faire apparaître des faces et de jolis polyèdres. Ceci respecte l'arrangement des atomes dans le système cristallin du minéral (diamant...) considéré. La cristallographie fait appel à deux disciplines des mathématiques
. la géométrie dans l'espace
. l'arithmétique
parce que les atomes sont placés à des multiples entiers (ou des sous-multiples simples) des dimensions d'une "maille", parallélépipède de base.
On étudie maintenant la cristallographie à grand renfort de groupes, autre discipline.
_________________
Il n'est pas du tout bizarre que MkNk, une droite du plan Pk soit perpendiculaire à (AG) : puisque (AG) est perpendiculaire à Pk elle est perpendiculaire (orthogonale) à toutes les droites du plan.
Oui, k = 1/2 pour être perpendiculaire à (BC)
Sympa la cristallographie
Pardon mais pourquoi (AG) est elle perpendiculaire à Pk?
Donc il n'y a qu'une valeur de k possible.
rappel :
Citation :
3) Prouver que I est le projeté orthogonal de A sur le plan (BDE)
3) Prouver que I est le projeté orthogonal de A sur le plan (BDE)
Cette réponse te suffit-elle ?
Pour la question4, comment faire?
je vois bien comment on calcule la distance mais la distance minimale
Tu calcules donc la distance (son carré suffira)
c'est bien sûr une fonction de k
Tu en cherches le minimum (minimum d'un trinôme du second degré en k...)
Et quand tu auras trouvé... tu te poseras la question de savoir si ce résultat est étonnant, c'est-à-dire si tu n'aurais pas pu le trouver autrement...
Je ne trouve pas comme toi
Je trouve que le trinôme est 6k2 - 6k + 2
et donc le minimum pour k = 1/2
Non, c'est bon, j'avais inversé (1-k) et (k-1)
Je trouve pareil
Bah en fait, on retrouve le même résultat que précédemment mais je vois pas trop ce que cela implique
Si k=1/2 alors (MkNk) perpendiculaire à (AG) et (BC)
La distance entre deux droites dans l'espace se mesure sur une perpendiculaire commune à ces deux droites. C'est pour cela que tu retrouves la réponse de la question précédente.
Tu me dis
Citation :
La distance entre deux droites dans l'espace se mesure sur une perpendiculaire commune à ces deux droites.
La distance entre deux droites dans l'espace se mesure sur une perpendiculaire commune à ces deux droites.
mais je ne vois pas pourquoi cela correspond à la distance minimale
La distance entre deux points est ... la distance minimale entre ces deux points
La distance entre deux droites est ... la distance minimale entre ces deux droites
ok
Un grand merci à toi Coll (j'ai appris plein de trucs )mais je sais pas si je vais continuer dans le diamant à force de voir de beaux diamants sans pouvoir en avoir....z'est trop inzuste
salut on a le meme sujet! et jaimerai bien savoir comment tu as pu calculer les coordonnées de I. merci
Bonjour,
Quelles sont les coordonnées des trois points, B, D et E, sommets du triangle BDE ?
Comment calcules-tu les coordonnées d'un isobarycentre de points dont tu connais les coordonnées ?
ben les points B,D et E ont pour coordonnées B(1,0,0) D(0,1,0) et E(0,0,1)
en fait j'ai le même sujet que Marie-C et je pige rien à ce sujet
La réponse à la première question posée à 8 h 31 est juste.
Quelle est la réponse à la deuxième question ? Un centre de gravité de triangle c'est l'isobarycentre des trois sommets.
hihi alala vaudrait peut-être que je revois mes leçons! je suisp perdu
sinon y a le sujet sur https://www.ilemaths.net/maths_t-sujet-bac-06-S-08.php
l'exercice 4
raaaa je sais vraiment pas comment calculer l'isobarycentre! peut-être que la formule suivante pourrait me servir:
GA+GB+GC=3GI 
Une "formule" doit aussi être comprise, ce qui permet de l'adapter au problème particulier posé.
Par définition du centre de gravité (ou isobarycentre) I du triangle BDE :
et donc (trois applications de la relation de Chasles) :
ce qui permet d'écrire :
Dans la base les coordonnées du vecteur
sont aussi celles du point I
Bonjour,
J'ai le même DM à rendre à la rentrée.
J'ai déjà pas mal avancée, mais j'ai quelques petits problèmes de résolution.
Déjà, pour l'équation du plan, je me suis servie de l'expression ax+by+cz+d=0 et j'ai trouvé x+y+z-1=0.
Est-ce bon ?
Pour les coordonnées de N(k) je me suis aidée de ce que vous aviez dit, mais je n'ai pas trop compris pourquoi y=3k-1.
Concernant la distance minimale, pourquoi utiliser seulement le carré, puisque la formule fait également intervenir une racine carrée. J'aurai donc penser à résoudre le polinôme, et ensuite ajouter une racine au résultat trouvé.
Et j'avoue avoir un peu de mal à tracer en annexe P (1/2) et la droite M(1/2) N(1/2).
Merci de votre aide.
Bonne journée.
Sandrine.
Bonjour,
Réponse à tes deux premières questions : mon message du 22/04/2007 à 08 h 31
Réponse sur la distance minimale : tu peux calculer le minimum de la distance si tu veux. Mais il est plus simple de chercher le minimum du carré de la distance. Personne ne t'oblige à te simplifier la vie...
J'ai bien vu votre message de 08h31.
Mais malgrès les explications données, j'ai du mal à comprendre pour le "y" :$
D'accord, donc enfaite, le k=1/2 est un carré ? Et si jamais je rajoute la racine, j'aurai alors calculé la valeur de la distance, pour k minimum, et non la valeur de k minimum ?
Ceci n'est pas l'équation d'une droite du plan xOy
Dans le plan xOy une droite a une équation
. soit de type y = ax + b
. soit de type x = a
Je t'ai posé une question à laquelle tu n'as pas encore répondu :
Citation :
Quelle est l'équation de la droite (BC) dans le plan xOy ?
Quelle est l'équation de la droite (BC) dans le plan xOy ?