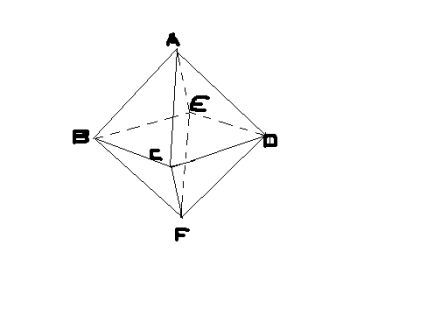
une petite aide serai la bienvenue je suis dessu depuis un bon moment
je sais qu'il faut que je prouve pour la question 1
si on prend comme vecteur directeur de (AF) vecteur AF
et deux vecteurs non colinéaires du plan BCDE par exemple vecteur CE et BD
IL faut prouvé AF.CE=0 et AF.BD=0 tous cela en vecteur biensur mais je sais pas comment le faire j'ai bien évidemment essayé plusieurs décomposition mais sans résultats

Bonjour,

la première question que l'on doit se poser est de savoir ce qu'est un octaèdre régulier.

C'est un polyèdre a 8 faces et ses 8 faces sont des triangles équilatéraux.

Ils sont forcément de même dimension, sinon il serait impossible de construire le polyèdre.

Comme ils sont de même dimension, tu peux affirmer que AB = BF.

Sans utiliser le produit scalaire, tu peux déduire facilement quelque chose sur le point B par rapport au segment [AF].

Non je vois pas trop comme nous sommes dans l'espace peut etre que le point B se trouve sur le plan médiateur du segment AF

c'est ça!!

Tu utilises ensuite le même raisonnement avec les points C, D et E

Oui je vois jen déduit qu'ils sont tous sur le plan médiateur de AF du méme coup ils appartiennent à un même plan c'est ça ?

oui et en plus ce plan est orthogonal à [AF].

Pas besoin de calculs compliqués avec le produit scalaire....

CE plan étan le plan médiateur est également perpendiculaire à AF

on a posté le message en meme temps je m'en suis aperçu ensuite merci
peut-tu m'aider pour la derniere question en me guidant également?

As-tu réussis à démontrer que BCDE est un carré?

non j'ai oublié désoLé.Euh... Je ne vois pas si on utilisé lé produit scalaire je diré qu'il fodrait prouvé BC.CD=0 et BE.ED=0 mais bon je ne vois pas non plus comment si on utilise ce que l'on a prouvé précédemment c'est a dire que les points B,C,D et E sont sur le plan médiateur de AF
JE bloque

Explique déjà que BCDE est un losange, c'est facile.

tout simplement BC=CD=DE=EB car les triangles sont équilatéraux de sommet A (ACD,AED etc)Je sais pas comment le dire exactement mais c'est un peu prè le principe

C'est ça, mais il faut rédiger en faisant des phrases correctes.

d'accord je le ferais.Pour prouvé que c'est un carré il faut ensuite que je prouve qu'il y a donc un angle droit?

oui je pense, mais je cherche...

ok j'ai pensé prouver que les diagonales c a dir BD et CE sont de meme longueur mais je ne vois pas comment

Je pense qu'il faut utiliser le milieu de [AF], tu peux l'appeler O. O est aussi le centre du losange BCDE. (il faudrait démontrer que avec le même raisonnement que (ACFE) est le plan médiateur de [BD] et que (ABFD) est le plan médiateur de [CE])

AOB est un triangle rectangle en O de même que AOC.

En utilisant Pythagore,tu as : AB²=OA²+OB² et AC²=AO²+OC².

Tu en déduis faciment que OB=OC.

Donc que les BD=EC.

Un losange qui a ses diagonales de même longueur est un carré.

(C'est une solution mais peut-être pas la meilleur)

daccor je vai lutilisé car je n'en vois pas d'autre merci

pour la seconde question as-tu une piste?

Quelle est la définition de 2 plans perpendiculaires?

si un plan P COntient une droite perpendiculaire à un autre plan P' alors ces plans sont perpendiculaires

Démontre alors que (ACF) est le plan médiateur de [BD] et le tour est joué.

sa ne pose pas de problème que D n'appartient pas au plan (ABF)?

Démontre que (ABFD) est le plan médiateur de [CE].
Cela impliquera que D appartient à ce plan.

Ok merci beaucoup pour ton aide précieuse je pensé devoir absolument m'en sortir avec les produits scalaires mais apparemment non.Bonne soirée

Au revoir.