M² = (x - x
Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
Produit scalaire dans l'espace "sphère"
Posté par iando95
Bonjour tout le monde je suis nouveau sur le site et j'aimerai savoir si on pourrait m'aider à résoudre cette exercice car je ne voit pas du tout comment faire ,surtout que mon prof a fait ce chapitre en 2h et la rangé sans même faire d'exercice d'application alors j'ai beaucoup de mal. Je vous remercie d'avance.
Les points Ω et A ont pour coordonnées :
Ω (2 ;-1 ;3) A(-1 ;0 ;1)
L'objectif de l'exercice étant de déterminer un équation de la sphère S de centre Ω et passant par A.
1 / Calculer ΩA
(Je ne vois pas ce qu'il veulent la distance ΩA surement mais quel formule nous permet de trouver ça.Moi dans mon cours il y seulement distance du point à une droite ...)
2 / M(x ;y ;z) est un point de S. Exprimer ΩM² en fonction de x, y, z
(J'ai pensé à ΩM² = (x-2;y+1;z-3)² mais je ne pense pas en réalité.)
3 / Dire que « M appartient à la sphère de centre Ω et de rayon ΩA » équivaut à dire que « ΩM² = ΩA² ».
Déduisez en une équation de la sphère S
(Il me faut les autres réponses pour pouvoir répondre à celle-ci)
c'est vrai je viens de remarquer j'avais pas pensé a cause du Z mais bon ...
donc on a :
=√(-1-2)²+(O+1)²+(1-3)²
=√14
Donc la distance ΩA est de √14.
Merci pgeod.
et mon idée pour la question 2 ?
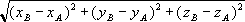
en utilisant la formule que tu m'as donné je trouve ça :
ΩM²=x²+y²+z²-4x+2y-6z+14
est-ce normal ?
...
On peut aussi l'écrire sous cette forme :
x(x-4)+y(y+2)+z(z-6)+14
en faisant ça je réponds bien à la question ?
ok je le laisse sous la forme initiale ...
et pour la question une équation de sphère c'est de quel forme ?
ΩM² = ΩA²
remplace ΩM² par l'expression qu'on vient de trouver
remplace ΩA² par sa valeur numérique.
...
(x -2)² +(y + 1)² + (z - 3)² = √14 =r²
donc au faite au final vu que ΩM² = ΩA² = r²
on retrouve l'équation cartésienne d'un cercle de centre Ω(2 ; -1 ; 3) et de rayon 14.
...
bah merci beaucoup de ton aide j'ai réellement bien compris le produit scalaire encore un ou deux exo et je suis prêt pour mon interro a + merci encore 