Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
Produit scalaire et ensembles de points
Posté par Tetsuka
Bonsoir à tous,
Pouvez vous me filer un petit coup de main pour résoudre cet exercice?
Citation :
A et B sont 2 points de l'espace tels que AB = 6cm
1) Soit (E) l'ensemble des points M de l'espace tels que Vec(MA).Vec(MB) = 7
a) Exprimer Vec(MA).Vec(MB) en fonction de MI et IA
b) Déterminer l'ensemble (E)
2) Soit (F) l'ensemble des points M de l'espace tels que MA2 + MB2 = 28
a) Exprimer MA2 + MB2 en fonction de MI et IA
b) Déterminer l'ensemble (F)
3) Soit (G) l'ensemble des points M de l'espace tels que MA2 - MB2 = -24
a) Démontrer que MA2 - MB2 = 2Vec(IM).Vec(AB)
b) Déterminer l'ensemble (G) en utilisant le projeté orthogonal de M sur (AB)
A et B sont 2 points de l'espace tels que AB = 6cm
1) Soit (E) l'ensemble des points M de l'espace tels que Vec(MA).Vec(MB) = 7
a) Exprimer Vec(MA).Vec(MB) en fonction de MI et IA
b) Déterminer l'ensemble (E)
2) Soit (F) l'ensemble des points M de l'espace tels que MA2 + MB2 = 28
a) Exprimer MA2 + MB2 en fonction de MI et IA
b) Déterminer l'ensemble (F)
3) Soit (G) l'ensemble des points M de l'espace tels que MA2 - MB2 = -24
a) Démontrer que MA2 - MB2 = 2Vec(IM).Vec(AB)
b) Déterminer l'ensemble (G) en utilisant le projeté orthogonal de M sur (AB)
Voilà, je ne sais pas comment démarrer... Je n'arrive pas à trouver de bonne solution avec la relation de Chasles...
Merci d'avance pour votre aide
Bonne nuit
I milieu de [AB] se traduit par la relation vectorielle
d'où on déduit que
et que
On rappelle aussi la relation entre produit scalaire, norme et longueur de segment
Donc on établit le résultat préliminaire suivant :
et comme dans cet exercice, AB=6
Résolution :
application de la relation de Chasles
développement de l'expression
simplification
Interprétation géométrique :
I étant le milieu du segment [AB] de longueur 6
les points M du plan vérifiant l'équation sont les points à distance 4 de I : c'est le cercle de centre I, de rayon 4
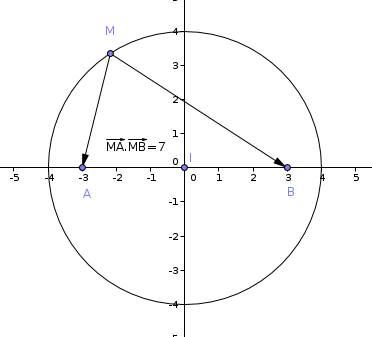
Allez, j'enchaine sur le 2) :
MA²+MB² = (MI+IA)²+(MI+IB)² = MI²+2MI.IA+IA² + MI²+2MI.IB+IB² = 2MI²+2MI(IA+IB)+IA²+IB²
Avec IA+IB = 0 et IA² = IB², donc
MA²+MB² = 2(MI²+IA²)
Et en valeurs, MA²+MB² = 28 et IA² = (6/2)² = 9, donc :
28 = 2(MI²+9)
MI² = 5
|MI| = 
5
F est un cercle de centre I et de rayon 5
Bonsoir, merci pour ton aide et tes explications, j'étais parti du mauvais côté comme on dit! En le refaisant tout seul, j'ai trouvé les mêmes résultats que toi.
Pour le 3, j'ai trouvé (G) le plan passant par H et perpendiculaire à (AB).
Et tu ne définis pas H ...
L'énoncé que tu as recopié disait :
a) Démontrer que MA² - MB² = 2Vec(IM).Vec(AB)
Rappel :
Citation :
I milieu de [AB], petit oubli de la part
I milieu de [AB], petit oubli de la part
Ca fait beaucoup d'imprécisions...
Le résultat est le plan perpendiculaire à la droite (AB) passant par ce milieu I du segment [AB].
Quand moi ou LeHibou parlons de cercle, traduire sphère.
Cette petite précision montre à quel point les techniques utilisées sont semblables, qu'on soit dans un plan ou dans l'espace.