Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
produits scalaire dans l'espace
Posté par inviteeee
Bonjour,
j'ai un exercice dans lequel on a un triangle rectangle en
tel que
. On a un point
qui se projette de manière orthogonale en
sur le plan
De plus
<= énoncé de l'exercice
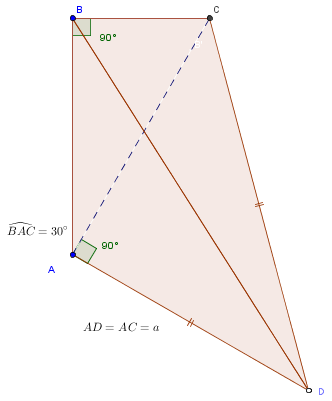
Etant donné que j'aborde le thème des produits scalaires dans l'espace en ce moment, j'en ai déduit cette figure mais je ne suis pas sure de sa justesse
Je dois calculer des produits scalaires qui sont:
Pourriez vous me dire si ma figure est juste par rapport aux donnés de l'énoncé car j'ai des doutes pour tenter de calculer ces produits scalaires, si la figure est déjà fausse, je n'aurais trouver que des réponses fausses .(et par la suite si ca ne vous déranges pas pourrais je vous donner après mes réponses pour que vous me dîtes si j'ai juste)
Merci de votre réponse 
Bon mes réponses sont les suivantes:
la première je n'ai pas trouvé le résultat
Qu'en pensez vous svp ?
(concernant ma figure je me suis demandé au final si elle ne doit pas être sur un plan ou si faire une figure dans l'espace reste la chose la plus juste):s
bonjour
ta figure est juste si tu peux remarquer que BAD=90°
qq indications:
AB.AC=||AB||*||AC||cos(BAC) ; tu termines les calculs
AB.AD=... ; sachant que (AB) perpendiculaire à (AD)
CD.CA=||CD||*||CA||cos(ACD) ; sachant que CA=AD=a et CAD=90°
AB.BD=||AB||*||BD||cos(ABD)
BC.CD=(BA+AC).(CA+AD) ; chasles
=BA.CA+BA.AD+AC.CA+AC.AD
=AB.AC-AB.AD-AC² ; car AC.AD=0
tu as déjà calculé AB.AC et AB.AD et tu as AC²=a²
Bonjour watik, merci de votre aide et de toutes vos indcations.
Je vais essayé de rédiger et de terminer les calculs sur ma feuille et si ca ne vous dérange pas je vous les posterez pour que vous me dîtes si ils sont justes ou totalement faux
Dsl si j'ai étais long mais je viens de me rendre compte que dans mon schéma j'ai mit que [CD]=[AD] alors que cest pas ca c'est [CA]=[AD].....j'ai mal placé les "traits m"arquand l'égalité.
Comme résultat j'ai trouvé:
....je n'arrive pas à trouver l'angle :s
et
mes résultats sont ils bon ? 
il y en a un que je n'ai pas réussi à terminer
Svp, j'ai refait les calculs et ceux que je vous ai mis sont faux pour certain et j'ai corrigé mes erreurs.
Pourriez vous juste m'aider pour prouver que car j'ai introduis des points(le point C par exemple) j'ai essayé et je n'y arrive pas :s, ainsi que pour
......j'ai calculer j'ai deja trouver que
et que BD=(\sqrt{13}a)/2...j'ai des doutes sur cette longeur
Merci d'avance de votre aide