Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Produits scalaires dans un cube

Posté par
ilemaths20 25-03-12 à 15:44

Bonjour,
j'ai fais cet exercice en cours récemment et je n'ai pas très bien compris, si quelqu'un pourrait le reprendre avec moi ça serait gentil

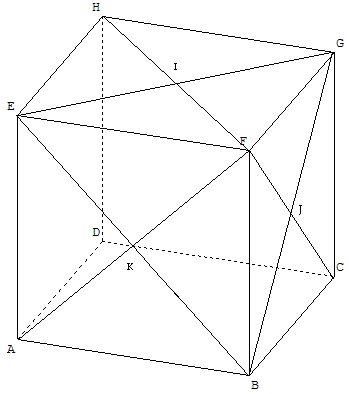
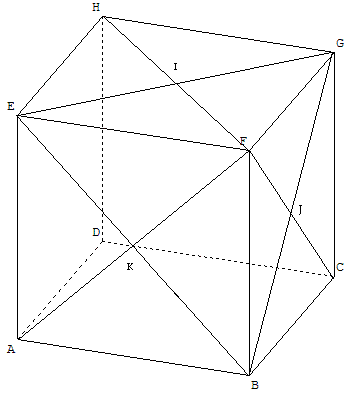
Enoncé : ABCDEFGH est un cube d'arête a. Les points I,J et K sont les centres respectifs des faces EFGH, GCBF et ABFE
Calculer les produits scalaires suivants :
1)
     AB . BH

2)
     AJ . BH

3)
     AG . BH
4)
     AD . BH

Merci

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 15:45

Voici la figure que j'ai oublié

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 15:45

Voici la figure que j'ai oublié

Produits scalaires dans un cube

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 16:15

Personne ne peut m'aider?

Posté par
dhaltere : Produits scalaires dans un cube 25-03-12 à 16:35

un produit scalaire dans l'espace euclidien suit les mêmes règles que dans le plan euclidien

tu connais les règles dans le plan ?

\vec{AB}.\vec{BH} = \vec{AB}.(\vec{BA}+\vec{AE}+\vec{EH})

tu développes
et tu remarques que certains vecteurs sont orthogonaux, alors leur produit scalaire est nul

il reste
\vec{AB}.\vec{BH} = \vec{AB}.\vec{BA}+0+0

si a=AB=||\vec{AB}||=\sqrt{\vec{AB}.\vec{AB}} est la longueur du segment AB, alors

\vec{AB}.\vec{BH} = -a²

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 16:49

Désolé mais je n'ai rien compris je suis largué
pourquoi AB.BH = AB(BA+AE+EH)?

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 17:04

Ah ca y est j'ai compris par contre je ne comprends pas pourquoi AB.EH est égale au vecteur nul?
C'est aussi orthogonaux?

Posté par
dhaltere : Produits scalaires dans un cube 25-03-12 à 17:06

parce que \vec{EH}=\vec{AD}

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 17:25

Et alors? que vient faire AD?

Posté par
dhaltere : Produits scalaires dans un cube 25-03-12 à 17:50

il est perpendiculaire à AB
youou, ici la terre

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 18:00

Mais pourquoi -a²??
moi j'aurais écris a²

Posté par
dhaltere : Produits scalaires dans un cube 25-03-12 à 18:11

tu as de vagues souvenirs sur les vecteurs et les produits scalaires dans le plan ?

tu devrais réviser cette partie avant d'espérer progresser

\vec{BA}=-\vec{AB}

\vec{AB}.\vec{AH}=\vec{AB}.\vec{BA} = -\vec{AB}.\vec{AB} = - a²

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 18:35

Ah d'accord j'essaye de faire le deuxième et je le poste
merci encore

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 19:38

Je ne vois pas comment faire avec AJ.BH ...
aide moi s'il te plait

Posté par
dhaltere : Produits scalaires dans un cube 25-03-12 à 20:08

L'idée dans ces exercices est de tout ramener aux vecteurs (\vec{AB},\vec{AD},\vec{AE})

quel intérêt ? ils sont orthogonaux deux à deux

pourquoi devrais-tu le savoir : parce que tu as fait la même chose l'année dernière avec des vecteurs dans le plan.

J centre de la face (BCGF) :

\vec{BJ}=\frac12(\vec{BC}+\vec{BF})

et puisque \vec{BC}=\vec{AD} et \vec{BF}=\vec{AE}

\vec{BJ}=\frac12(\vec{AD}+\vec{AE})

\vec{AJ}=\vec{AB}+\vec{BJ}=\vec{AB}+\frac12(\vec{AD}+\vec{AE})

j'accélère, fais un effort de ton coté

\vec{BH}=-\vec{AB}+\vec{AD}+\vec{AE}

d'où le produit scalaire
\vec{AJ}.\vec{BH}=(\vec{AB}+\frac12(\vec{AD}+\vec{AE})).(-\vec{AB}+\vec{AD}+\vec{AE})

on développe et on ne garde que les termes qui ne sont pas nuls du fait des vecteurs orthogonaux :

\vec{AJ}.\vec{BH}=-a²+\frac12a²+\frac12a²=0

les deux droites (AJ) et (BH) sont perpendiculaires.Produits scalaires dans un cube

Posté par
ilemaths20re : Produits scalaires dans un cube 25-03-12 à 20:47

Je reprendrai l'exercice demain
merci beaucoup encore à toi
bonne soirée


Rechercher
Menu
Espace membre
18 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !