Niveau terminale

Projeté orthogonal et produit scalaire

Posté par
KingFrieza 21-03-09 à 14:23

Bonjour, je n'arrive pas à comprendre cet exercice. Pourriez-vous m'aider s'il vous plait, merci

EXERCICE :

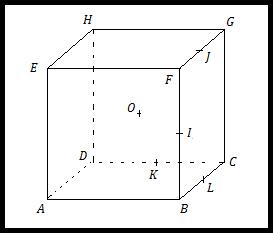
On considère un cube ABCDEFGH de côté a.

Les points I, J, K, L et O sont les milieux respectifs de [BF], [FG], [CD], [BC] et [AG].

1. Déterminons le projeté orthogonal de J sur (AB). Déduisons-en $\vec{AJ}.\vec{AB}$ .

2. Déterminons de même :

$\vec{DJ}.\vec{DC} ; \\ \\ \vec{HA}.\vec{HB} ; \\ \\ \vec{BI}.\vec{BH} ; \\ \\ \vec{BJ}.\vec{BL} ; \\ \\ \vec{FG}.\vec{EG} ; \\ \\ \vec{DK}.\vec{DI}$

Merci encore pour votre future aide

Projeté orthogonal et produit scalaire

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 14:46

Voilà, j'ai essayé pour la 2. Dites-moi si c'est juste.

$\vec{DJ}.\vec{DC} = a^2$

$\vec{HA}.\vec{HB} = 2a^2$

$\vec{BI}.\vec{BH} = \frac{1}{2}a^2$

$\vec{BJ}.\vec{BL} = \frac{1}{4}a^2$

$\vec{FG}.\vec{EG} = a^2$

$\vec{DK}.\vec{DI} = \frac{1}{4}a^2$

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 15:29

je crois qu'il y a une petite erreur dans la dernière, refais-le

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 15:33

$\vec{DK}.\vec{DI} = \frac{1}{2}a^2$

Sinon, tout le reste est juste ?

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 15:41

j'ai pas trouvé d'autre erreur, mais je ne suis pas infaillible^^. Par contre, même si je suis bien d'accord que c'aurait été très fastidieux, il faudra justifier chacune de tes égalités. Mais je pense bien que si tu as tous ces résultats c'est que tu as compris comment il fallait faire

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 15:47

Oui, j'ai juste marqué ce que j'ai trouvé ici. Sinon j'ai les intermédiaires. Pour preuve :

$\vec{DK}.\vec{DI}=\vec{DK}.(\vec{DC}+\vec{CB}+\vec{BI})$

$\vec{DK}.\vec{DI}=\vec{DK}.\vec{DC}+\vec{DK}.\vec{CB}+\vec{DK}.\vec{BI}$

$\vec{DK}.\vec{DI}=\frac{1}{2}a^2 + 0 + 0$

On retrouve bien : $\red \fbox{\vec{DK}.\vec{DI}=\frac{1}{2}a^2}$

Pourriez-vous m'aider pour le 1. s'il vous plait ? Merci

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 16:04

oui, ou si tu sais te servir des plans tu peux juste mettre DK.DC+DK.CI
avec DK est un vecteur normal à la face du cube qui sontient CI

Bah pour le 1 c'est pareil Si tu projettes orthogonalement J sur (AB) tu trouves p(J)=B car BCGF orthogonal à (AB)
donc AJ=AB+BJ avec BJ.AB=0

Posté par re : Projeté orthogonal et produit scalaire 21-03-09 à 16:05

Merci beaucoup Jean-Claude ! C'est très gentil de m'avoir aidé. J'ai compris

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Produit scalaire en terminale
3 fiches de mathématiques sur "produit scalaire" en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

5 visiteurs

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Projeté orthogonal et produit scalaire

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths