Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
QCM Produit scalaire dans le plan
Posté par Adeoap
Bonjour
Nous avons un QCM à faire pour la rentrée. Mon prof de l'année dernière n'a pas fait la fin du programme (barycentre, produit scalaire, équation de cercle).
Je ne vois donc absolument pas comment répondre au QCM. Peut être qu'en comprenant la première question, je verrais comment faire la suite.
La voici :
"1) AB.AD est égal :
* 0
* 16
* 4
2) CA.CD est égal à :
* 0
* 16
* 16V2
3) OB.OD est égal à :
* 8
* 0
* -8
4) OB.OC est égal à :
* 8
* -8
* 0"
La figure correspondante est la suivante :
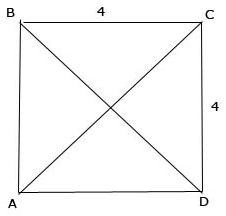
Je crois avoir trouvé le petit 1) à partir d'une formule trouvée sur internet, mais la méthode me semble un peu longue.
1) AB.AD = (1/2)(||AB + AD||² - ||AB||² - ||AD||²)
AB.AD = (1/2) ((4 + 4)² - 4² - 4²)
AB.AD = (32/2) = 16
Pour la suite, je ne vois pas.
Merci d'avance.
Bonjour
le 1, cela fait 0
car les deux vecteurs sont orthogonaux, et le produit scalaire de 2 vecteurs orthogonaux est nul
Bonjour, non est perpendiculaire à
donc
(tu parles bien de vecteurs ?)
pour CA.CD tu décomposes CA en CD+DA, ça donne (CD+DA)CD=CD² (l'autre est nul car les vecteurs sont perpendiculaires) = 16
J'ai oublié de préciser : sur ma figure, O correspond au centre du carré. Je parle bien de vecteurs, je n'ai juste pas pris la peine de mettre les flèches.
Merci beaucoup pour vos réponses, j'y vois plus clair, j'ai refait les calculs en détaillant chez moi.
Par contre, comment procède-t-on pour le petit 3) ?
OB et OD sont deux vecteurs égaux et opposés de longueur 2
2 (la moitié de la diagonale d'un carré de coté 4) donc leur produit scalaire vaut -OB²= -8
J'ai un autre petit problème sur cette question.
""
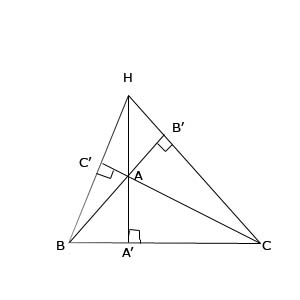
Que signifient les barres au dessus de A'B et A'C, par exemple ?
Merci
c'est la 2e possibilité
produit des mesures algébriques, vectAB donne AB(barre) que je garde, et je projette le second vecteur sur le premier
donc vectAC donne AB' (barre)
on conserve l'un et on projette l'autre sur celui qui est conservé
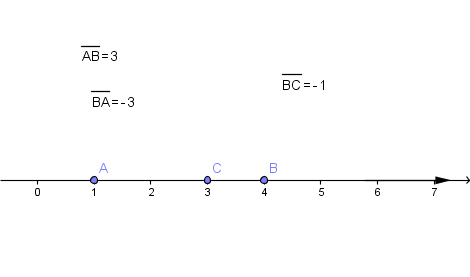
la barre signifie qu'on prend un sens sur la droite support, c'est donc un axe
et suivant le sens choisi, tu peux trouver AB(barre) = "+ qq chose" ou "- la même chose", dit autrement, la distance entre A et B précédée d'un signe + ou d'un signe -, ou encore xB-xA
projeter : c'est le projeté orthogonal d'un point sur une droite
ici, si tu projettes C sur la droite (BB'), tu trouves B' car (CB') est perpendiculaire à (BB') et A est invariant par cette projection
ça va ?
Pour la projection, j'ai compris; pour la barre, non : n'aurais-tu pas un cours qui l'explique ?
Merci encore pour ton aide.