Inscription / Connexion Nouveau Sujet
Représentation graphique d'une fonction Sup
Coucou,
Alors voilà j'ai une fonction f(x) = sup(-x+1, -x2-2x+8) à représenter mais je ne sais pas comment m'y prendre puisque je n'ai jamais rencontrer ce type de fonction.
Je sais que sup correspond à supérieur mais je ne vois pas du tout à quoi cela peut correspondre.
Est-ce qu'il faut que je représente -x+1 puis -x2-2x+8 ?? mais si je fais ça quelle serait l'utilité du sup ?
Dernière question : Est-ce que ma calculatrice Casio 35+ sait représenter cette fonction un peu particulière ? et si oui comment ?
Merci pour toute aide apportée.
Bonjour,
Il faut commencer par résoudre l'inéquation -x+1>-x2-2x+8
Si on note S les solutions de cette inéquation (c'est une réunion de 2 intervalles), alors :
-> si x
S, f(x)=-x+1
-> si x
S, f(x)=-x2-2x+8
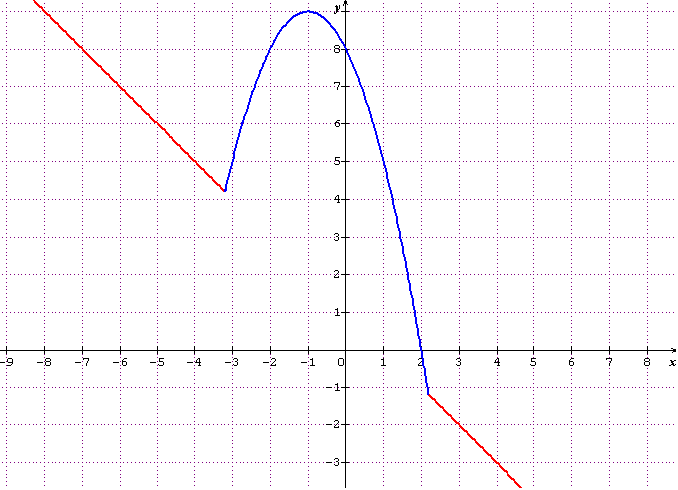
Voici la courbe obtenue :
pour résoudre l'inéquation, on passe tout du même côté et ensuite on utilise le discriminant ?
du genre : -x+1 > -x2-2x+8
x2+x-7 >0
= 29
et donc 1ère solution : x1 = ( -1-
29 ) /2
2ème solution : x2 = ( -1+29 ) /2
Et donc S = ]-
; x1] U [x2;+[
Est-ce correct ?
Normalement je n'ai pas le droit d'utiliser ma calculatrice, donc je ne vois pas comment je peux tracer la courbe puisque je ne connais pas la valeur exacte de 29. C'est impossible de la tracer..
Il suffit de tracer la droite d'équation y=-x+1 et la parabole d'équation y=-x²-2x+8 et de ne conserver, pour chacun des 3 intervalles, que la courbe qui est au-dessus de l'autre. Où est la difficulté ?
Annuler
connectez vous
analyse en post-bac