Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Master Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Master
Partager :

Résidus d'un pôle

Posté par
gaara 10-12-12 à 21:11

Bonsoir,

J'ai un problème avec un exercice :
on a une fonction :
\\ h(z) = \pi \frac{cotan(\pi z)}{z^2} = \pi \frac{cos(z\pi)}{z^2sin(z\pi)} \\

J'ai calculer les pôles j'ai trouvé :
z_1 = 0 d'ordre 3
z_2 = k avec k \in \mathbb{Z}

l'ordre de 0 c'est bien 3??

pour calculer Res(h, 0) j'ai fait :
\\ Res(h, 0) = \lim_{z\to 0} \frac{1}{2} (z^3 h(z))^{''} \\
mais ça me donne ce truc incalculable :

\\ = \frac{-\pi^2}{2} \lim_{z\to 0} (\frac{2}{sin^2(z\pi)} - \frac{2z\pi cos(z\pi)}{sin^3(z\pi)}) \\

Comment je fais pour calculer le résidus en 0 SVP? merci

Cordialement

Posté par
GaBuZoMeure : Résidus d'un pôle 10-12-12 à 21:18

En tout cas, pas par la formule que tu emploies. D'où sort-elle ?
Un petit coup de développement limité devrait te permettre de t'en sortir. N'oublie pas que tu cherches le coefficient de 1/z dans le développement en série de Laurent.

Posté par
miltonre : Résidus d'un pôle 10-12-12 à 21:19

salut
si t'est vraivent en troisieme année tu doi pouvoir calculer tte limite

Posté par
GaBuZoMeure : Résidus d'un pôle 10-12-12 à 21:22

@milton : et toi, tu devrais pouvoir écrire sans faire une faute tous les deux mots.

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 21:31

GaBuZoMeu

Merci, ça me rassure, je vais suivre cette piste

Posté par
miltonre : Résidus d'un pôle 10-12-12 à 21:38

tu pourais pousser tes recherches sur la frequence de mes fautes

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 21:45

j'ai pas trouvé la série de Laurent de cotan(z), c'est quoi ???

Posté par
GaBuZoMeure : Résidus d'un pôle 10-12-12 à 21:54

Tu dois connaître les développements limités en 0 de cos et sin, non ? (il n'y a pas besoin d'aller bien loin ici).

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 22:08

j'ai trouvé sur le net que :

\\ \pi cot(z\pi) = \frac{1}{z} + \sum_{-\infty}^{+\infty} \frac{1}{z+n} \\

donc

\\ \\ h(z) = \frac{1}{z^3} + \sum_{-\infty}^{+\infty} \frac{1}{z^3+z^2n} \\ \\

mais y a pas le terme 1/z;

pour les développements limités en 0 de cos et sin, je ne sais pas à quel terme je vais m'arrêter ??

Posté par
GaBuZoMeure : Résidus d'un pôle 10-12-12 à 22:18

Plutôt que de piocher sur le net, mets-toi au travail pour de bon ! Essaie, et tu verras.

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 22:19

J'ai trouvé une autre formule de cot :

\\ cot(z) = \frac{1}{z} - \frac{z}{3} - \frac{z^3}{45} ... \\

donc :

\\ h(z) = \frac{1}{z^3} - \frac{\pi^2}{3z} - ... \\

donc le Res(h, 0) = \frac{-\pi^2}{3} ??

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 22:20

c'est que j'ai jamais fait le développement limité, c'est pour ça j'ai du mal à ma retrouvé

Posté par
GaBuZoMeure : Résidus d'un pôle 10-12-12 à 22:28

Et ce n'est pas en piochant sur le net que tu vas apprendre ! Tu iras aussi surfer sur internet pendant l'examen ?
Quelle formation as-tu suivie pour ne jamais avoir fait de dl ? J'ai peine à imaginer que ça soit possible.

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 22:41

j'ai fait licence maths et informatique, du coups on a sacrifier plusieurs modules de maths malheureusement,
voila ce que j'ai trouvé en utilisant le développement limité
je ne sais pas si mon raisonnement est correcte, voila ce que j'ai fait :
au voisinage 0 on a :
\\ \\ h(z) = \frac{\pi}{z^2} \frac{cos(z\pi)}{sin(z\pi)} \\      \\      = \frac{\pi}{z^2} \frac{1 - \frac{(z\pi)^2}{2}}{z\pi} \\      \\      = \frac{1}{z^3} - \frac{\pi^2}{2z} \\ \\
donc le Res(h, 0) = -\frac{\pi^2}{2}

>_<

Posté par
GaBuZoMeure : Résidus d'un pôle 10-12-12 à 22:55

La, tu étais trop court en développement limité. Ce que tu as écrit (avec des signes =, sans écrire le reste du dl) est incorrect. Il faut TOUJOURS garder trace de ce qu'on néglige, sinon on fait des erreurs; la preuve. Essaie de faire mieux, pour retomber sur ton premier résultat.

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 23:01

Merci infiniment, ça ma trop aidé, je vais réessayer

Posté par
gaarare : Résidus d'un pôle 10-12-12 à 23:58

j'ai fait le dl à l'ordre 3 j'ai trouvé :

\\ \\ = 1/z^3 - \pi^2/(3z) - \pi^4z/12 \\ \\

et c'est le bon résultat j'imagine

Posté par
GaBuZoMeure : Résidus d'un pôle 11-12-12 à 08:13

je n'ai pas vérifié le dernier terme, ça va pour le résidu mais encore une fois, tu n'écris pas "=" si tu omets le reste !

Posté par
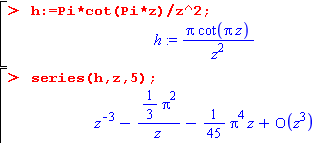
gaarare : Résidus d'un pôle 11-12-12 à 14:32

Bien reçu! merci

Posté par
GaBuZoMeure : Résidus d'un pôle 11-12-12 à 14:46

Maple n'est pas d'accord avec toi :

Résidus d\'un pôle


Rechercher
Menu
Espace membre
4 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !