Inscription / Connexion Nouveau Sujet
Bonsoir,
La suite définie initialement vérifie:
et
.
La suite définie par jsvdb vérifie:
et
.
Bien que les deux suites vérifient la même relation de récurrence, , ce ne sont pas les mêmes suites.
La méthode est bonne et j'ai trouvé d'où provient le problème. Tout ce que je t'ai dit dans mon précédent post est correct.
Ce qui se passe, est que nous avons , qui est inférieur à
, donc on se trouve directement dans la zone croissante. Donc ce qui a été fait est correct.
Il y a aussi le cas que j'avais testé (en fait c'était une erreur), c'était de prendre pour une valeur comprise entre
et
au lieu de
qui correspond à la zone décroissante.
On constate ceci dans le tableau XLS (de jsvdb), en commençant avec , nous obtenons
car dans cette zone la suite est décroissante, normalement on devait commencer avec
. Une fois on calcule
on se retrouve dans la zone croissante et on y reste jusqu'à convergence.
Désolé d'avoir semé le doute.
Désolé d'avoir semé le doute.
Non vous n'avez pas à être désolé, au moins vous m'avez appris une nouvelle méthode pour traiter les suites. Merci !
Mais ça veut dire que tout ce qu'on a fait depuis le début est faux ?
Il y a des inexactitudes dans ce qu'a dit ... Razes

Il a avancé qu'il y avait une discussion selon
 . J'ai montré que non.
. J'ai montré que non.
jsvdb a étayé expérimentalement cette démonstration. Expérimenter n'est pas démontrer, mais les exemples pris par jsvdb sont éclairants.
Razes montre que le sujet aurait pu être pris par un autre biais. C'est vrai, mais ce qu'il annonce comme méthode plus simple nécessite un changement de variable, pas nécessairement immédiat. Son idée est néanmoins intéressante car elle montre que l'on pourrait fabriquer d'autres exercices sur le même thème en choisissant les fonctions f et g avec les "bonnes" propriétés.
Il n'y a donc aucun souci avec la démonstration finale que j'ai proposée.
Je précise ce que j'ai voulu dire le 17-09-16 à 23:05.
La définition de la suite donnée par tuxedo95 le 15-09-16 à 17:52 ne devait pas être la bonne. Je la rappelle:
et pour
:
.
Avec cette définition on calcule:
etc...
Or n'est défini que si
c'est-à-dire, après étude d'une fonction, si
.
Quand cette condition est vérifiée, pour
.
La suite est bien définie, elle est croissante et elle converge vers .
Avec cette définition la suite n'est pas définie si .
Mais jsvdb a donné une autre définition le 17-09-16 à 10:13:
en posant
.
Cela revient à modifier la définition de tuxedo en posant: et pour
:
.
Avec cette définition la suite est bien définie pour tout et elle converge vers
.
Pour compléter on peut montrer que la convergence de la suite est "quadratique":
.
Il y a eu pas mal de définition de f. Alors dans l'ordre :
En étudiant la fonction
On pose
La fonction est
Puis j'ai repris cette dernière le 17-09-16 à 10:13 lieu de poursuivre dans la mienne.


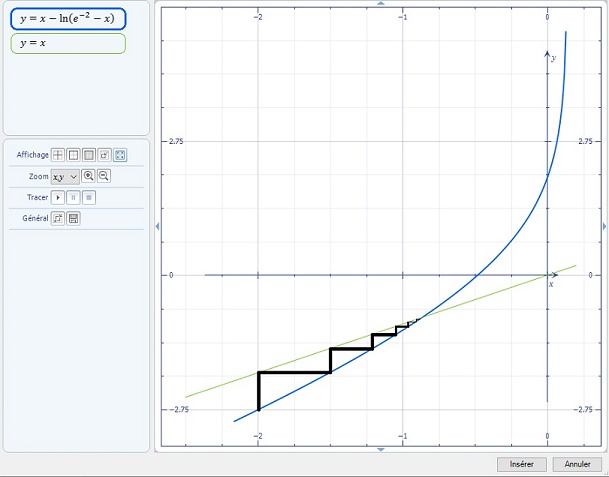

 analyse en post-bac
analyse en post-bac