Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques

1 2 +

Niveau Maths sup
Partager :

Séries numériques

Posté par
tuxedo95 15-09-16 à 17:52

Bonjour,
Je reviens vous embêter avec les suites et séries numériques
Enoncé:
Soit \lambda > 0. Soit, (z_n)_{n\ge2}  définie par z_1 = ln(\lambda)
et n 2.   z_n = \sum_{k=1}^{n-1} ln(\lambda - z_k)
Etudier (z_n)

Je suis un peu bloqué face à un tel énoncé, une idée qui me passe par la tête est d'appliquer la fonction exp mais je suis pas sûr de moi.

Merci d'avance

Posté par
jsvdbre : Séries numériques 15-09-16 à 18:34

Bonjour tuxedo95

Je te propose déjà de commencer par te demander si la série est définie pour tout > 0. Et si la réponse est non, de déterminer pour quels la série est définie.

Posté par
boninmire : Séries numériques 15-09-16 à 18:39

L'idée la plus immédiate est d'étudier la différence de deux termes consécutifs.

Posté par
tuxedo95re : Séries numériques 15-09-16 à 19:18

@jsvdb  la série est définie pour tout \lambda > z_k . C'est tout ce que je peux vous dire

@boninmi : si je ne me trompe pas, z_{n+1} - z_n = ln(\lambda - u_n)

Posté par
boninmire : Séries numériques 15-09-16 à 20:08

Tu veux dire ln(-zn).
Sauf erreur de ma part, on montre que cette différence est positive en utilisant l'inégalité
ln()≤-1
visible sur le graphique, et en raisonnant par récurrence.
Il me semble donc que cette suite est croissante.

Posté par
carpediemre : Séries numériques 15-09-16 à 20:31

salut

tuxedo95 @ 15-09-2016 à 19:18

@jsvdb  la série est définie pour tout \lambda > z_k . C'est tout ce que je peux vous dire   


super !!!

la question est de savoir si un terme étant calculé peut-on calculer le suivant !!!

j'utilise a à la place de lambda ...

z_1 existe pas définition de la suite

puis-je calculer z_2 ?

si oui puis-je continuer ?

boninmi donne une propriété utile de la fonction ln dans son dernier post

d'ailleurs ln x < x suffit même peut-être ....

Posté par
tuxedo95re : Séries numériques 15-09-16 à 21:08

Oula oui, en fait je viens de réaliser que c'est une suite, car dans ma tête c'était une série donc j'étais parti pour étudier sa convergence , comme on fait pas mal de séries en ce moment je me mélange un peu les pinceaux, cela dit pour la définition de la suite (z_n)
doit-on montrer qu'elle existe par récurrence sur n  ?

Posté par
tuxedo95re : Séries numériques 15-09-16 à 21:11

Je comprends pourquoi vous m'avez suggéré l'inégalité ln(x) < x mais à partir de n = 3 les logarithmes comment à s'imbriquer les uns dans les autres, ça rend l'étude de définition un peu plus complexe

Posté par
tuxedo95re : Séries numériques 15-09-16 à 21:40

@boninmi, je sais pas comment vous faites mais pour la récurrence je pose P(n) : '' ln(\lambda - z_n) > 0 "
et pour montrer P(n+1) c'est compliqué parce que je pars de ln(\lambda - z_{n+1}) = ln(\lambda - (z_n + ln(\lambda - z_n))) et jusqu'ici je n'avance plus car je ne connais pas le signe de z_n

Posté par
Razesre : Séries numériques 15-09-16 à 22:50

En calculant z_2, on trouve: z_2=\ln(\lambda -\ln(\lambda ))

En étudiant la fonction f(x) = \ln(x-\ln(x)), on constate qu'il y a un point critique qui correspond à x=1.

Donc on doit discuter la valeur de \lambda:

a) \lambda\in]0,1[
b) \lambda=1
c) \lambda\in]1,\+\infty[

Posté par
jsvdbre : Séries numériques 15-09-16 à 23:10

C'était à ça que je pensais en postant la première réponse.
Et une récurrence forte montre que pour \lambda = 1, la suite (z_n) est nulle. A vérifier.

Posté par
tuxedo95re : Séries numériques 15-09-16 à 23:14

D'accord, je vais méditer sur ces mots

Posté par
Razesre : Séries numériques 15-09-16 à 23:26

Pour \lambda = 1, la suite z est nulle.

Je pense que pour les autres valeurs possibles, il faut voir dans quel intervalle on se trouve et en tirer les conclusions.

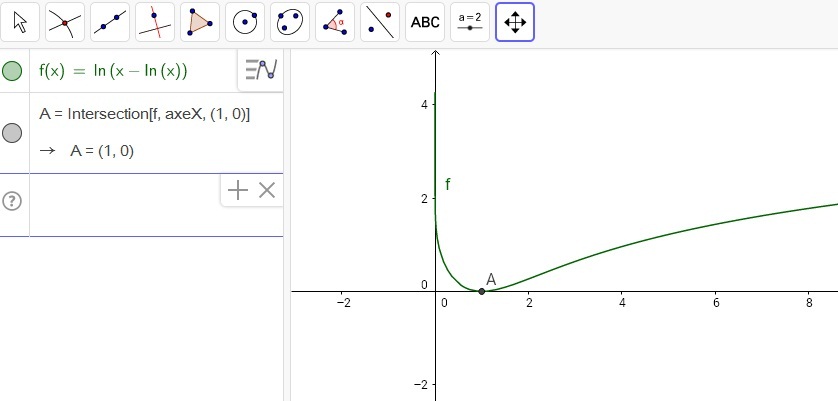
Séries numériques

Posté par
jsvdbre : Séries numériques 15-09-16 à 23:29

@razes : quel est le logiciel que tu utilises ?

Posté par
Razesre : Séries numériques 15-09-16 à 23:40

jsvdb @ 15-09-2016 à 23:29

@razes : quel est le logiciel que tu utilises ?
geogebra

Posté par
carpediemre : Séries numériques 15-09-16 à 23:58

il serait peut-être utile d'écrire en extension les quatre premiers termes de la suite

z_1 = \ln a

z_2 = \ln(z1 - a) = \ln(a - \ln a)

z_3 = \ln (a - z_1) + \ln(a - z_2) = \ln(\ln(a - \ln a)) + \ln(a - \ln a)

z_4 = ...

z_n = \sum_1^{n - 1} f(z_k}) avec f(x) = \ln (x - \ln x)

....

Posté par
jsvdbre : Séries numériques 16-09-16 à 03:17

Je vais être un peu contrariant, car la fonction qu'il faut étudier n'est pas  Ln(x - Ln(x)).

On pose f(x) = Ln(\lambda - x) \textrm { pour } x \in D_{\lambda} = ]- \infty, \lambda}[ et on a, en remarquant que 0 \in D_{\lambda}

z_1 = Ln(\lambda) = f(0)

Ensuite, formellement :

On désigne la nième composée de f par f^{(n)}

z_2 = Ln(\lambda - z_1) = f(z_1) = f^{(2)}(0)

z_3 = Ln(\lambda - z_1) + Ln(\lambda - z_2) = f(0) + f^{(2)}(0) = \lambda_1

z_4 = Ln(\lambda - z_1) + Ln(\lambda - z_2) +Ln(\lambda - z_3) = \lambda_1 + f(\lambda_1) = \lambda_2

z_5 = Ln(\lambda - z_1) + Ln(\lambda - z_2) +Ln(\lambda - z_3) +Ln(\lambda - z_4)  = \lambda_2 + f(\lambda_2)

***

z_n = z_{n-1} + f(z_{n-1})  \forall n \geq 3

\textrm {Et donc, \red SI la limite l existe, elle vérifie en vertu de la continuité de f : } l = l + f(l) \textrm { c'est-à-dire : } l=\lambda-1

\textrm {On retrouve bien la limite nulle pour } \lambda = 1

Maintenant, on revient à mon premier post : quelles sont les valeurs de \lambda pour lesquelles la suite z est définie ?

Ma conjecture est : toutes les valeurs de strictement positives.

Posté par
boninmire : Séries numériques 16-09-16 à 11:04

jsvdb @ 16-09-2016 à 03:17


Maintenant, on revient à mon premier post : quelles sont les valeurs de \lambda pour lesquelles la suite z est définie ?

Ma conjecture est : toutes les valeurs de strictement positives.

C'est ce que dit l'énoncé ...

Posté par
jsvdbre : Séries numériques 16-09-16 à 12:02

Bonjour Boninmi

Je me permets de ne pas être d'accord.
En effet, l'énonce laisse entendre à priori que la suite est bien définie pour tout \lambda. Mais le même énoncé continu :

tuxedo95 @ 15-09-2016 à 17:52

Etudier (z_n)

De nature plutôt réticent avec les affirmations péremptoires, il m'a semblé de bon ton de vérifier.
En fait, la suite (z_n) est une suite (z_n(\lambda)).

Je me propose de le faire de la façon suivante :

Soit donc \lambda > 0.

z_1, z_2 et z_3 sont clairement définis.

On suppose alors, qu'il existe un entier n \geq 3 tel que z_n soit défini. Montrons que z_{n+1} est défini.

Mais, le fait que z_n soit défini implique que f(z_{n-1}) soit défini et donc que z_{n-1} < \lambda.

Question donc : est-ce que z_{n} < \lambda ?

On sais que f(z_{n-1})= Ln(\lambda - z_{n-1}) < \lambda - z_{n-1} d'où z_n = z_{n-1} + f(z_{n-1}) < \lambda

Je peux donc dire que f(z_{n}) existe et que par suite, z_{n+1} aussi.

Conclusion, l'affirmation péremptoire ... n'est plus péremptoire !

Reste maintenant à voir pour quels \lambda il existe une limite.

Posté par
boninmire : Séries numériques 16-09-16 à 15:51

jsvdb @ 16-09-2016 à 12:02

Bonjour Boninmi

Je me permets de ne pas être d'accord.
En effet, l'énonce laisse entendre à priori que la suite est bien définie pour tout \lambda.

Je ne comprends pas ta remarque.
L'énoncé commence par "Soit >0".
Il ne me semble donc pas que l'énoncé laisse entendre que la suite est bien définie pour tout \lambda.
Tout à fait d'accord avec toi par contre sur la nécessité de justifier que la suite est bien définie pour >0, ce que tu as fait.

Posté par
boninmire : Séries numériques 16-09-16 à 16:23

Nous sommes d'accord sur

zn=zn-1+ln(-zn-1)

Or si f(x)=x+ln(-x)
l'étude de cette fonction montre que f(x)≤-1
sur le domaine de définition x<.

En particulier
zn=f(zn-1)≤-1

On en déduit (sans récurrence d'ailleurs) que zn+1-zn≥0
Le suite est donc croissante au sens large.
Reste à examiner si elle est majorée ou pas selon .

Posté par
jsvdbre : Séries numériques 16-09-16 à 16:53

boninmi @ 16-09-2016 à 15:51


Il ne me semble donc pas que l'énoncé laisse entendre que la suite est bien définie pour tout \lambda.
Tout à fait d'accord avec toi par contre sur la nécessité de justifier que la suite est bien définie pour >0, ce que tu as fait.

Ah ! ok ! simple malentendu.

Posté par
boninmire : Séries numériques 16-09-16 à 17:02

jsvdb @ 16-09-2016 à 16:53


Ah ! ok ! simple malentendu.

Quant à moi, je n'ai pas les yeux en face des trous.
Je viens de montrer, sauf erreur, que zn≤-1
La suite est donc majorée. Croissante et majorée, elle a une limite, qui est, comme tu as dit plus haut, -1 .

Posté par
jsvdbre : Séries numériques 16-09-16 à 17:24

Moi aussi, j'ai loupé le fait que j'avais montré à 16-09-16 à 12:02, que zn < . Ce qui est moins précis que toi, mais suffisant.
Bravo à toi pour la simplicité !

On peut peut-être continuer l'exo en posant f() = Lim zn() = - 1 et étudier une éventuelle convergence uniforme ? Ce qui serait surprenant, intuitivement, compte tenu du domaine non borné de f. A voir !

En revanche, ce qui peut être plus intéressant c'est d'essayer de conclure quelque chose du genre  : \sum_{k=1}^{\infty}{\dfrac {1}{\lambda -z_k}} = 1 (par étude de "dérivée de la somme" = "somme des dérivée" !)

Posté par
boninmire : Séries numériques 16-09-16 à 17:57

tuxedo95 va peut-être nous dire s'il y a une suite ...

Posté par
Razesre : Séries numériques 16-09-16 à 17:57

z_{n+1} = \sum_{k=1}^{n} \ln(\lambda - z_k)\Rightarrow z_{n+1}-z_n = \ln(\lambda - z_n)   (1)

Si la suite z a une limite l, alors on passe à la limite de (1), ce qui nous donne: \lambda=l+1

Posté par
jsvdbre : Séries numériques 16-09-16 à 18:19

boninmi @ 16-09-2016 à 17:57

tuxedo95 va peut-être nous dire s'il y a une suite ...

Allez Tuxedo95, la suite ... on est curieux de savoir pour la CVU et la dérivation

Posté par
Razesre : Séries numériques 16-09-16 à 18:26

Razes @ 15-09-2016 à 22:50

Donc on doit discuter la valeur de \lambda:

a) \lambda\in]0,1[
b) \lambda=1
c) \lambda\in]1,\+\infty[


a) La suite diverge
b) la suite est constante = 1
c) la suite converge vers \lambda-1

Posté par
Razesre : Séries numériques 16-09-16 à 18:33

a) Pose \lambda=0.2 et calcule z_3 et z_4

Posté par
carpediemre : Séries numériques 16-09-16 à 19:00

bon je suis et je dois dire :

beau travail collaboratif et beau développement  

je m'étais trompé dans la fonction qu'on itère ... mais le fait d'écrire en extension les premiers termes permet de voir efficacement ce qui se passe et introduire la bonne fonction ...

Posté par
Razesre : Séries numériques 16-09-16 à 19:04

La fonction est f(x)=x+\ln(\lambda-x), il faut l'étudier dans l'intervalle a)

Mais pour la partie c) une fois on commence à calculer les 1er terme \lambda-u_k devient négatif.

Posté par
boninmire : Séries numériques 16-09-16 à 20:54

Razes @ 16-09-2016 à 18:26

Razes @ 15-09-2016 à 22:50

Donc on doit discuter la valeur de \lambda:

a) \lambda\in]0,1[
b) \lambda=1
c) \lambda\in]1,\+\infty[


a) La suite diverge
b) la suite est constante = 1
c) la suite converge vers \lambda-1
Razes @ 16-09-2016 à 19:04

La fonction est f(x)=x+\ln(\lambda-x), il faut l'étudier dans l'intervalle a)

Mais pour la partie c) une fois on commence à calculer les 1er terme \lambda-u_k devient négatif.

Je ne vois pas comment tu justifies.
f(x) est toujours majorée par -1. Cela ne dépend pas de .
Par ailleurs zn+1=f(zn)
La suite est donc majorée par -1.
Enfin, zn+1-zn=ln(-zn)
zn≤-1
zn-≤-1
-zn≥1
ln(-zn)≥0
et la suite est donc croissante.
La suite étant croissante et majorée, elle a une limite.
Où y a-t-il à discuter selon ?
Sauf erreur de ma part à me préciser.

Posté par
tuxedo95re : Séries numériques 16-09-16 à 21:03

jsvdb @ 16-09-2016 à 18:19

boninmi @ 16-09-2016 à 17:57

tuxedo95 va peut-être nous dire s'il y a une suite ...

Allez Tuxedo95, la suite ... on est curieux de savoir pour la CVU et la dérivation


Malheureusement les matheux, j'aimerais prolonger le plaisir mais il n'y pas d'autre question.
Merci à vous tous d'y avoir consacré du temps pour m'aider
vous êtes formidables !

Posté par
tuxedo95re : Séries numériques 16-09-16 à 21:04

Désolé j'ai fini l'école à 19h donc je n'ai pu vous répondre que maintenant

Posté par
tuxedo95re : Séries numériques 16-09-16 à 22:19

Voici le devoir rédigé, bien sûr je n'ai pas fait de " copié collé ", je me suis servi de vos propositions seulement comme base de réflexion.

Montrons la suite (z_n) est définie n 2 et \lambda > 0
On a  z_n = \sum_{k=1}^{n-1} ln(\lambda - z_k) = z_{n-1} + ln (\lambda - z_{n-1}) = f(u_{n-1})
Montrons par récurrence sur n l'existence de (u_n)
Soit P(n) : " \lambda \ge z_{n-1}" 2
Initialisation .....
Hérédité:

On a f(z_{n-1})= Ln(\lambda - z_{n-1}) \le \lambda - z_{n-1} d'où z_n = z_{n-1} + f(z_{n-1}) \le \lambda
=> \lambda  \ge z_n

Conclusion :  z_{n+1} existe, P(n+1) vraie
Donc P(n) est vraie (z_n) est définie n 2

Ainsi d'après l'étude de la fonction f(x) = x + ln(\lambda - x) on trouve que (z_n) est croissante et majorée  et \lim_{n\to +\infty} z_n  = \lambda - 1

Voilà le compte rendu, qu'en pensez vous ?

Posté par
tuxedo95re : Séries numériques 16-09-16 à 22:20

tuxedo95 @ 16-09-2016 à 22:19

Voici le devoir rédigé, bien sûr je n'ai pas fait de " copié collé ", je me suis servi de vos propositions seulement comme base de réflexion.

Montrons la suite (z_n) est définie n 2 et \lambda > 0
On a  z_n = \sum_{k=1}^{n-1} ln(\lambda - z_k) = z_{n-1} + ln (\lambda - z_{n-1}) = f(u_{n-1})
Montrons par récurrence sur n l'existence de (u_n)
Soit P(n) : " \lambda \ge z_{n-1}" 2
Initialisation .....
Hérédité:

On a f(z_{n-1})= Ln(\lambda - z_{n-1}) \le \lambda - z_{n-1} d'où z_n = z_{n-1} + f(z_{n-1}) \le \lambda
=> \lambda  \ge z_n

Conclusion :  z_{n+1} existe, P(n+1) vraie
Donc P(n) est vraie (z_n) est définie n 2

Ainsi d'après l'étude de la fonction f(x) = x + ln(\lambda - x) on trouve que (z_n) est croissante et majorée  et \lim_{n\to +\infty} z_n  = \lambda - 1

Voilà le compte rendu, qu'en pensez vous ?

Posté par
Razesre : Séries numériques 16-09-16 à 23:15

Oui. Pour le cas a) \lambda\in]1,\+\infty[
b) \lambda=1 la suite est constante z_n=0; \forall n\in\mathbb{N}
c) as tu calculé z_1, z_2, z_3, z_4, pour  \lambda\in]0,1[; prends par exemple  \lambda=0.1 pour voir ce qui se passe. (c'est pas beaucoup de travail mais tu seras fixé.

Posté par
Razesre : Séries numériques 17-09-16 à 00:15

Razes @ 16-09-2016 à 17:57

z_{n+1} = \sum_{k=1}^{n} \ln(\lambda - z_k)\Rightarrow z_{n+1}-z_n = \ln(\lambda - z_n)   (1)

Si la suite z a une limite l, alors on passe à la limite de (1), ce qui nous donne: \lambda=l+1

J'ai vérifié mes notes. La suite est convergente pour \lambda\in]0,+\infty[ et sa limite est \lambda-1.

Posté par
jsvdbre : Séries numériques 17-09-16 à 10:13

Effectivement, le problème posé est équivalent à celui-ci :

\textrm {Soit } \lambda > 0, f \textrm { la fonction définie par } f(x) = x + Ln(\lambda - x). \textrm { Étudiez la suite paramétrée suivante : }

\begin{cases} z_0 = 0& \text{ si } n= 0 \\ z_n = f(z_{n-1}) & \text{ si } n > 0 \end{cases}

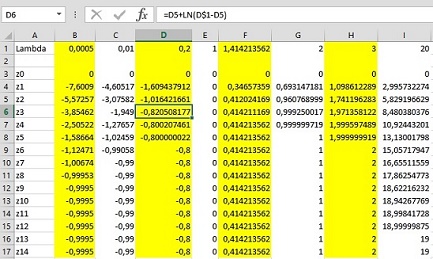
Avec une belle image pour étayer la thèse que la suite converge pour tout \lambda > 0 vers \lambda - 1. Ce qui nous fixe définitivement.

Séries numériques

Posté par
boninmire : Séries numériques 17-09-16 à 11:51

Razes @ 16-09-2016 à 23:15

Oui. Pour le cas a) \lambda\in]1,\+\infty[
b) \lambda=1 la suite est constante z_n=0; \forall n\in\mathbb{N}
c) as tu calculé z_1, z_2, z_3, z_4, pour  \lambda\in]0,1[; prends par exemple  \lambda=0.1 pour voir ce qui se passe. (c'est pas beaucoup de travail mais tu seras fixé.
Razes @ 17-09-2016 à 00:15

Razes @ 16-09-2016 à 17:57

z_{n+1} = \sum_{k=1}^{n} \ln(\lambda - z_k)\Rightarrow z_{n+1}-z_n = \ln(\lambda - z_n)   (1)

Si la suite z a une limite l, alors on passe à la limite de (1), ce qui nous donne: \lambda=l+1

J'ai vérifié mes notes. La suite est convergente pour \lambda\in]0,+\infty[ et sa limite est \lambda-1.

Mon raisonnement étant valable pour tout >0 et pour tout n, il est clair qu'il n'y avait pas de discussion selon , excepté la condition posée dès le départ par l'énoncé (>0).

Cordialement.

Posté par
tuxedo95re : Séries numériques 17-09-16 à 14:56

Un énorme MERCI à Razes  à jsvdb et à Boninmi ainsi qu'à d'autres membres du forum d'avoir apporté votre génie pour résoudre mon problème de façon claire et précise.

MILLE MERCIS

Posté par
boninmire : Séries numériques 17-09-16 à 15:04

Posté par
Razesre : Séries numériques 17-09-16 à 17:28

tuxedo95 @ 17-09-2016 à 14:56

Un énorme MERCI à Razes  à jsvdb et à Boninmi ainsi qu'à d'autres membres du forum d'avoir apporté votre génie pour résoudre mon problème de façon claire et précise.

MILLE MERCIS
Bonjour tuxedo95 , Bonjour à tous,
J'ai essayé de voir si une autre solution existe, effectivement l y a moyen de simplifier la résolution, en opérant un changement de variable:

u_n=z_n-\lambda+1

u_{n+1}-u_n=\ln(1-u_n); ainsi on est débarrassé de \lambda
De là on peut étudier les fonctions g(x)=\ln(1-x) et aussi f(x)=x+\ln(1-x).

Un tableau de variation serait de g(x) serait d'une grande utilité. On verra que la suite est décroissante sur sur ]0,1[ et croissante sur ]-\infty,0[;

On s'apercevra que si le premier terme de la suite démarre dans l'intervalle ]0,1[, à partir d'un certain rang elle basculera dans l'intervalle  ]-\infty,0[ jusqu'à convergence.

Posté par
Razesre : Séries numériques 17-09-16 à 20:43

\begin{array}{|c|ccccc||}\hline\hline x&-\infty&&0&&1\\\hline g'(x)=\dfrac{1}{x-1}& &&-&&\\\hline\hline g(x)=\ln(1-x)&+\infty &\searrow&0 &\searrow&-\infty\\\hline\end{array}

u_{n+1}-u_n=g(u_n); Le fait que u_n soit croissante ou décroissante, dépends des premiers termes de la suite (soit ils sont dans  ]-\infty,0[ ou  ]0,1[ , (voir tableau de variation de g(x))

Posté par
tuxedo95re : Séries numériques 17-09-16 à 21:50

Bonsoir Razes

Je pense que la dérivée de g(x) c'est plutot g'(x) = \frac{-1}{1-x}  non ?
du coup g serait croissante sur les 2 intervalles

Posté par
tuxedo95re : Séries numériques 17-09-16 à 21:52

non j'ai rien dit désolé

Posté par
tuxedo95re : Séries numériques 17-09-16 à 21:59

Mais ça veut dire que tout ce qu'on a fait depuis le début est faux  ?

Posté par
tuxedo95re : Séries numériques 17-09-16 à 22:17

Je ne comprends plus rien, je ne vois aucune faute dans ce qu'on a fait avec les autres, de plus, vous avez dit Razes :

Razes @ 17-09-2016 à 20:43


u_{n+1}-u_n=g(u_n); Le fait que u_n soit croissante ou décroissante, dépends des premiers termes de la suite (soit ils sont dans  ]-\infty,0[ ou  ]0,1[ , (voir tableau de variation de g(x))


Or regardez le tableur que nous a montré
jsvdb @ 17-09-2016 à 10:13



Séries numériques


pour \lambda = 0,2 par exemple, z_1 < 0 pourtant la suite (z_n) semble être croissante

Posté par
Razesre : Séries numériques 17-09-16 à 22:18

tuxedo95 @ 17-09-2016 à 21:59

Mais ça veut dire que tout ce qu'on a fait depuis le début est faux  ?
En partie, car il y a eu beaucoup d'échanges de commentaires.

Mais, ceci te permettra d'aborder le sujet autrement. En passant par un changement de suites u_n=z_n-\lambda+1 ou v_n=z_n-\lambda au choix. Ce qui simplifierait la résolution avec des études de fonctions.

Posté par
tuxedo95re : Séries numériques 17-09-16 à 22:28

Razes regardez mon post précédant, je suis un peu sceptique de votre solution

1 2 +


Rechercher
Menu
Espace membre
15 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1729 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !