Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Somme de nombres complexes

Posté par
needer 09-03-19 à 16:57


Bonjour,

Soient : z,\zeta \in \mathbb{C}, z\overline{\zeta }=i,   m\ge 3,  \displaystyle\omega ={{e}^{\frac{2\pi i}{m}}}

Je cherche à trouver :

                                                       \frac{1}{m}{{\sum\limits_{0\le j<m}{\left|z+{{\omega }^{j}}\zeta  \right|}}^{2}}\left({{\omega }^{j}}-{{\omega }^{-j}} \right)

Donc:

\begin{aligned}  \frac{1}{m}{{\sum\limits_{0\le j<m}{\left|z+{{\omega }^{j}}\zeta  \right|}}^{2}}\left( {{\omega }^{j}}-{{\omega }^{-j}} \right)&=\frac{1}{m}{{\sum\limits_{0\le j<m}{\left| z+{{\omega }^{j}}\zeta  \right|}}^{2}}{{\omega}^{j}}-\frac{1}{m}{{\sum\limits_{0\le j<m}{\left|z+{{\omega }^{j}}\zeta  \right|}}^{2}}{{\omega }^{-j}} \\   & =\frac{1}{m}\sum\limits_{0\le j<m}{\left( z+{{\omega }^{j}}\zeta  \right)\left( \overline{z}+\overline{{{\omega }^{j}}}\overline{\zeta } \right){{\omega }^{j}}}-\frac{1}{m}\sum\limits_{0\le j<m}{\left( z+{{\omega }^{j}}\zeta  \right)\left( \overline{z}+\overline{{{\omega }^{j}}}\overline{\zeta } \right){{\omega }^{-j}}} \\   & =\frac{1}{m}\sum\limits_{0\le j<m}{\left(\left( {{\left| z \right|}^{2}}+{{\left| \zeta  \right|}^{2}} \right){{\omega }^{j}}+\overline{z}\zeta {{\omega }^{2j}}+z\overline{\zeta } \right)}-\frac{1}{m}\sum\limits_{0\le j<m}{\left( \left( {{\left| z \right|}^{2}}+{{\left| \zeta \right|}^{2}} \right){{\omega }^{-j}}+z\overline{\zeta }{{\omega }^{-2j}}+\overline{z}\zeta  \right)}  \end{aligned}

Comme :

   \displaystyle \sum\limits_{0\le j<m}{{{\omega }^{j}}=\frac{1-{{\omega }^{m}}}{1-\omega }}=0$   et   $\displaystyle \sum\limits_{0\le j<m}{{{\omega }^{2j}}=\frac{1-{{\omega }^{2m}}}{1-{{\omega}^{2}}}}=0

\displaystyle \sum\limits_{0\le j<m}{{{\omega}^{-j}}}=\sum\limits_{0\le j<m}{{{\left(\overline{\omega } \right)}^{j}}}=\frac{1-{{\left(\overline{\omega }\right)}^{m}}}{1-\overline{\omega }}=0   et    \displaystyle \sum\limits_{0\le j<m}{{{\omega}^{-2j}}}=\sum\limits_{0\le j<m}{{{\left(\overline{\omega }\right)}^{2j}}}=\frac{1-{{\left( \overline{\omega} \right)}^{2m}}}{1-{{\left( \overline{\omega }\right)}^{2}}}=0

Donc:
                               \frac{1}{m}{{\sum\limits_{0\le j<m}{\left|z+{{\omega }^{j}}\zeta  \right|}}^{2}}\left({{\omega }^{j}}-{{\omega }^{-j}}\right)=i+i=2i

Y a-t-il des erreurs,  je vous remercie d'avance.


Posté par
carpediemre : Somme de nombres complexes 09-03-19 à 17:46

salut

le cheminement du calcul semble convenable ... mais je ne vérifierai pas ...

quelques remarques (pour être plus efficace) :

1/ pourquoi s'emmerder avec ce facteur 1/m ? (on peut toujours diviser par m en fin de calcul)

2/ à la fin de ton développement des deux sommes j'aurai tout regroupé en une somme en sachant que

z \bar y = i \iff \bar z y = -i

on peut alors factoriser simplement (il me semble)

Posté par
neederre : Somme de nombres complexes 09-03-19 à 18:00


Bonjour carpediem;

Merci pour vos remarques, je vais les prendre en compte, voir même plus.

Mais le but est de savoir si la réponse finale est juste ou pas, si j'ai réussi à vérifier le calcul avec le logiciel de calcul formel Maple, je ne poste pas la question ici.

Posté par
neederre : Somme de nombres complexes 09-03-19 à 18:11

carpediem @ 09-03-2019 à 17:46


... mais je ne vérifierai pas ...


Pourquoi critiquer si tu n'as pas envie de calculer et vérifier ?

Posté par
neederre : Somme de nombres complexes 09-03-19 à 18:16


Et si moi j'ai envie de m'emmerder avec  \frac{1}{m} , j'ai le droit ou pas ?
Je suis amoureux de cette  \frac{1}{m} .

Posté par
neederre : Somme de nombres complexes 09-03-19 à 18:21


Et si tu ne le savais pas en maths, il y a plusieurs façons de raisonnées, l'essentiel c'est que ces raisonnements soient logiques et la réponse finale juste.

Posté par
carpediemre : Somme de nombres complexes 09-03-19 à 20:22

needer @ 09-03-2019 à 18:21


Et si tu ne le savais pas en maths, il y a plusieurs façons de raisonnées, l'essentiel c'est que ces raisonnements soient logiques et la réponse finale juste.
bien d'accord ... mais ici ce n'est pas du raisonnement mais du calcul !!!

et il y a plusieurs façons de calculer ...

moi je choisis toujours la simplicité et l'efficacité ... parce que plus c'est simple ... ben moins c'est compliqué !!!

en particulier moins j'ai de symboles inutiles moins j'ai de (mal)chance de me tromper ...

needer @ 09-03-2019 à 18:11

carpediem @ 09-03-2019 à 17:46


... mais je ne vérifierai pas ...


Pourquoi critiquer si tu n'as pas envie de calculer et vérifier ?
ben non je ne critique pas je dis simplement
needer @ 09-03-2019 à 18:00


Merci pour vos remarques, je vais les prendre en compte, voir même plus.

Mais le but est de savoir si la réponse finale est juste ou pas, si j'ai réussi à vérifier le calcul avec le logiciel de calcul formel Maple, je ne poste pas la question ici.
ce ne sont donc que des remarques pour être plus efficace (voir plus haut) et me simplifier la vie ...

de plus avec des formules plus simples peut-être que Maple saura justement le faire ...

Posté par
carpediemre : Somme de nombres complexes 09-03-19 à 20:40

soit y, z \in \C  /  z\bar y = i et m > 2 et w = ...

|z + yw^j|^2 = (z + yw^j)(z^* + y^*w^{-j}) = zz^* + yy^* + zy^*w^{-j} + z^*yw^j \\ \\ |z + yw^j|^2 (w^j - w^{-j}) = (zz^* + yy^*)(w^j + w^{-j}) + zy^*w^{-2j} + z^*yw^{2j}

puis après on somme ... série géométrique ...

ce que je ne comprends pas c'est que si toutes tes "sommes géométriques" sont nulles comment tu trouves au final i + i

Posté par
neederre : Somme de nombres complexes 09-03-19 à 21:19

Tu préfères les détails comme un élève de collège OK :

                                                             \begin{aligned} \\ \frac{1}{m}{{\sum\limits_{0\le j<m}{\left| z+{{\omega }^{j}}\zeta  \right|}}^{2}}\left( {{\omega }^{j}}-{{\omega }^{-j}} \right)&=\frac{1}{m}\sum\limits_{0\le j<m}{z\overline{\zeta }}-\frac{1}{m}\sum\limits_{0\le j<m}{\overline{z}\zeta } \\ \\ & =\frac{1}{m}mz\overline{\zeta }-\frac{1}{m}m\overline{z}\zeta  \\ \\ & =z\overline{\zeta }-\overline{z}\zeta  \\ \\ & =i-\left( -i \right) \\ \\ & =i+i \\ \\ & =2i   \\ \end{aligned}

                       Car  :  z\overline{\zeta }=i\Rightarrow \overline{z\overline{\zeta }}=\overline{i}\Rightarrow \overline{z}\zeta =-i

Posté par
carpediemre : Somme de nombres complexes 09-03-19 à 21:23

Posté par
neederre : Somme de nombres complexes 09-03-19 à 21:25


Encore plus de détail ? Il y a toujours moyen en maths, on reste ici toute la nuit, pas de souci

Posté par
carpediemre : Somme de nombres complexes 09-03-19 à 22:07

bren disons que si tu arrives à lire ce que tu as écrit tant mieux ....

Posté par
perroquetre : Somme de nombres complexes 10-03-19 à 01:20

Bonjour, needer.

Je te confirme l'exactitude de ton calcul.

Bonjour, carpediem.

Le 9 mars 2019, à 20h40, tu as écrit:

Citation :

|z + yw^j|^2 = (z + yw^j)(z^* + y^*w^{-j}) = zz^* + yy^* + zy^*w^{-j} + z^*yw^j \\ \\ |z + yw^j|^2 (w^j - w^{-j}) = (zz^* + yy^*)(w^j + w^{-j}) + zy^*w^{-2j} + z^*yw^{2j}


Il y a des fautes dans ta deuxième ligne. On a en fait:

|z + yw^j|^2 (w^j - w^{-j}) = (zz^* + yy^*)(w^j - w^{-j}) - zy^*w^{-2j} + z^*yw^{2j} + zy^* -z^*y

Et en sommant, on obtient le même résultat que needer.

Posté par
carpediemre : Somme de nombres complexes 10-03-19 à 08:35

ha oui merci

j'ai oublié le moins du deuxième facteur !!

Posté par
neederre : Somme de nombres complexes 10-03-19 à 20:14


Bonjour perroquet,  Merci pour ta confirmation.

Posté par
neederre : Somme de nombres complexes 10-03-19 à 20:16

Bonjour carpediem,

carpediem @ 09-03-2019 à 22:07

bren disons que si tu arrives à lire ce que tu as écrit tant mieux ....


Je ne sais pas pourquoi le latex n'affiche pas le code, mais voici une image :

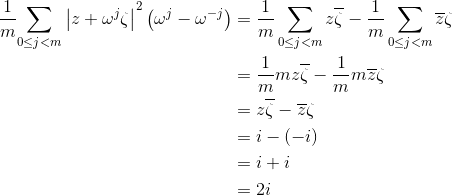
Somme de nombres complexes

Posté par
carpediemre : Somme de nombres complexes 10-03-19 à 20:25

merci ...

modulo mon erreur de signe on arrive au même résultat ...


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !