- Arithmétique : divisibilité, PGCD et PPCM, Nombres premiers
- Des mathématiciens célèbres : Fermat et Gauss
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
--> Pk : " x = ck appartient à C "pour tout k appartenant à N
si c'est vrai pour tout k alors il n'y a plus rien à montrer !!

Je crois que sa propriété est uniquement la partie entre guillemets. Mais c'est effectivement ambigu !
Ce que veut dire carpediem, c'est que ta propriété doit bien être
Pk: "ck appartient à c", et non pas Pk = "ck appartient à c pour tout k dans N".
Écris plutôt : pour tout k dans N, montrons Pk : "ck appartient à c".
Si j'écris la propriété suivante :
Pk : x=ck appartient à C pour tout k appartenant à N.
Est ce juste ?
Pour la 2), écris x = qc + r la division euclidienne de x par c, et montre que r est nul. Commence par montrer que r est dans C.
Voilà ma réponse au 3) :
c | x implique que c = x
Or, c appartient à cZ
Donc, x appartient à cZ
Comme x appartient à C, cZ = C
Voila ma réponse pour le 2), n'hésitez pas à me faire part de mes erreurs :
*Soit x appartenant à C
*Comme x appartient à C et cZ est inclus dans C, il existe k appartenant à Z tel que x=ck
*Comme x = ck = ck + 0, c divise x par définition
* Division euclidienne de x par c avec q appartenant à Z:
x = cq + 0
et 0 <= 0 < | c |
Attention, tu confonds inclusion et égalité d'ensembles.
On dit que A est inclus dans B si tout élément de A appartient à B. Mais ça ne veut pas dire que les ensembles sont égaux, tu peux avoir des éléments dans B qui ne sont pas dans A. Par exemple, mais tu n'as pas égalité
Tu as pris x un élément quelconque de C et montré qu'il était dans cZ, ça démontre que tout élément de C est dans cZ, donc seulement que C est inclus dans cZ.
En revanche, à la question 1), tu avais déjà montré que cZ est inclus dans C, et si A est inclus dans B (tout élément de A est dans B) et B inclus dans A (tout élément de B est dans A), alors A = B.
Donc tu peux conclure que C = cZ, mais seulement en utilisant la question 1).
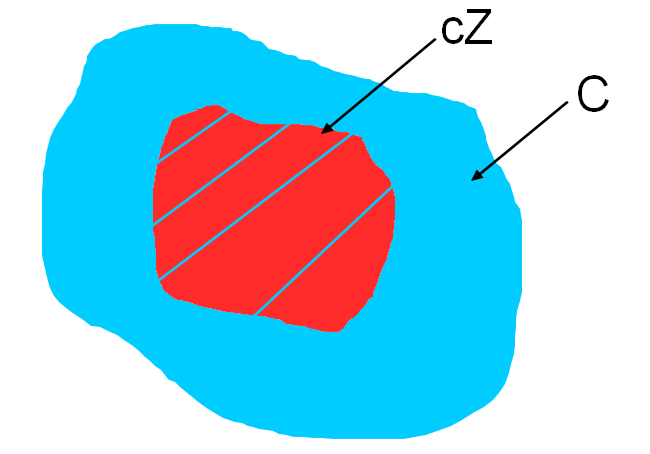
Même confusion pour la question 2). Vois la figure ci-dessous, cZ inclus dans C ne veut pas dire que tous les éléments de C ont la forme kZ. Seulement que tous les éléments de la forme kZ sont dans C. Tu pourrais a priori avoir des éléments de C qui ne s'écrivent pas du tout kZ.
Bonjour,
As-tu réussi à montrer que le reste dans la division euclidienne de x par c est dans C ?
C'est la première étape.
Tout d'abord dois-je poser la division euclidienne suivante (?) :
x = qc + r ( q appartenant a Z et r a N ).
Ensuite, on a x qui appartient C ( cf énoncé ).
De plus, qc appartient a C ( avec q appartenant à Z ) car c appartient C.
Comme x = qc + r alors r appartient à x ?
Je pense cela bien faux et mal rédigé.... dites moi ce que vous en pensez, merci.
Donc mon raisonnement est bon?
A quoi cela me sert de dire que r appartient a C si je considère ensuite que r vaut 0?
Tu dois montrer que r vaut 0. Ce n'est pas encore fait !
Juste pour vérifier que tu as compris, quelle propriété est-ce que tu utilises pour déduire que r est dans C ?
J'ai raisonné ainsi:
On pose : x = qc + r (q appartient a Z et r a N)
Donc r = x - qc.
Or, x appartient a C et qc appartient a C avec q appetant a Z car c appartient c.
Donc x - qc appartient a C et par conséquent ( comme r = x - qc ) r appartient a C.
N'ayant jamais fait ce genre d'exercice auparavant, je reste septique face à la rédaction et à la rigueur de mes explications...
Donc mon raisonnement est bon?
A quoi cela me sert de dire que r appartient a C si je considère ensuite que r vaut 0?
Je ne vois pas ou vous voulez en venir, pouvez vous le donnez les étapes respectives et surtout leur intérêt afin je puisse comprendre et si jamais je bloque sur une je vous ferai appel. Merci
Ne t'inquiète pas, tu y es!
On a donc c le plus petit élément de . Et r un élément de
strictement inférieur à c. Que peux-tu en déduire sur r ?
(Si jamais tu ne vois pas, tu peux supposer par l'absurde que r est non nul et ça tombe tout seul).
Je vois ou vous voulez en venir : r serait égale à zéro, mais comment peut on en être sur? Ça ne serait pas supposer que tout les éléments constituant C sont strictement positifs? Or il est bien écrit que dans l'énoncé que C est un sous groupe de Z ???
Donc j'imagine le cas ou c= - 6 alors :
0=< r < | - 6 |
Je dois sûrement faire une erreur dans mon raisonnement, n'hésitez pas à me le faire remarquer et je ne sais pas si toutes les questions que je me pose sont légitimes ou non. Merci beaucoup pour votre attention!
Tu as étudié ce qu'est un sous-groupe ?
Un sous-groupe additif vérifie une propriété dite de "stabilité par passage à l'opposé" :
Donc dès que ,
est non vide, et son plus petit élément c est forcément positif.
Je ne suis qu'en terminale donc je n'ai, moi non plus, pas étudié les sous groupes. Donc toute ces notions me paraissent ambiguës. Cependant, cet exercice nous est bel et bien demandé donc je m'efforce tout de même à trouver une solution.
C'est assez ridicule de vous donner sous ces conditions un exercice pareil... Tu ne devrais plus avoir trop de problèmes à finir, mais n'hésite pas si tu as encore des questions ou veux qu'on vérifie tes raisonnements !


