Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Suite à termes complexes

Posté par
Ramanujan 17-09-18 à 17:48

Bonjour,

Soit (z_n) la suite définie par z_0 = r e^{i \theta}, où r \in \R^+ et \theta \in ]- \pi , \pi[ et la relation de récurrence :

\forall n \in \N , z_{n+1} = \dfrac{|z_n|+z_n}{2}

Démontrer que cette suite converge vers un nombre complexe que l'on précisera.

J'essaie d'appliquer la définition du cours :
(z_n) converge vers un nombre complexe a si (|z_n-a|) converge vers 0.

Mais ici je n'ai pas la suite (z_n)

Posté par
Glapion Moderateurre : Suite à termes complexes 17-09-18 à 17:58

Bonjour, moi je poserais z_n = r_n e^{i\theta_n}}
et j'essaierais de trouver une relation entre rn+1 et rn et aussi entre les en utilisant la relation de récurrence.

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 18:04

Ok merci Glapion, je vous posterai ce que j'ai trouvé.

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 18:24

z_{n+1}=r_{n+1}e^{i \theta_{n+1}} = \dfrac{r_n +r_{n}e^{i \theta_{n}}}{2}

Donc :

r_{n+1}e^{i \theta_{n+1}} = r_n \dfrac{1 +e^{i \theta_{n}}}{2}

D'où :

r_{n+1}e^{i \theta_{n+1}} = r_n e^{i \dfrac{\theta_n}{2}} \times  \dfrac{e^{-i \dfrac{\theta_n}{2}} +e^{i \dfrac{\theta_n}{2}}}{2} =  r_n e^{i \dfrac{\theta_n}{2}}  cos( \dfrac{\theta_n}{2})

Donc : \theta_{n+1} = \dfrac{\theta_n}{2}} et r_{n+1}= r_n cos( \dfrac{\theta_n}{2})

Ainsi : \theta_{n}  = \theta_{0} (\dfrac{1}{2})^n = \theta (\dfrac{1}{2})^n  

Soit : r_{n+1}= r_n cos(  \theta (\dfrac{1}{2})^n  )

Je vois pas comment calculer r_n

Posté par
Glapion Moderateurre : Suite à termes complexes 17-09-18 à 18:48

tu peux toujours itérer et dire que
rn =r cos cos(/2) .... cos(/2n)

et puis je crois qu'il y a une formule pour calculer ce produit de cosinus ça vaut
sin cos /(2n sin(/2n)

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 18:49

r_{n+1}= r_n cos( \dfrac{\theta}{2^n}})

Ce n'est pas une suite géométrique donc je bloque.

Posté par
larrechre : Suite à termes complexes 17-09-18 à 18:59

Bonsoir,

Vous aurez , sauf erreur, r_{n}= r\prod_{k=1}^{n} cos( \dfrac{\theta}{2^k} )

Le calcul du produit est un classique, exprimer chaque terme en fonction du sinus de l'angle double

(en complément de ce qu'a déjà dit Glapion et à seule fin de ne pas avoir écrit ça pour rien)

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 19:01

r_{n+1}= r_n cos( \dfrac{\theta}{2^n}})

Or : r_{n}= r_{n-1} cos( \dfrac{\theta}{2^{n-1}}})

Donc : r_{n}= r_{n-2}  cos( \dfrac{\theta}{2^{n-1}}}) cos( \dfrac{\theta}{2^{n-2}}})

Par itération je trouve :

r_n =r_{n-n} cos( \dfrac{\theta}{2^{n-1}}}) cos( \dfrac{\theta}{2^{n-2}}}) \times ... \times cos( \dfrac{\theta}{2^{n-n}}})

Soit : r_n =r cos( \dfrac{\theta}{2^{n-1}}}) cos( \dfrac{\theta}{2^{n-2}}}) \times ... \times cos( \dfrac{\theta}{2^{0}}})

Soit : r_n = r \prod_{k=0}^{n-1} cos( \dfrac{\theta}{2^{k}}})

C'est juste ?

C'est juste ?

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 19:05

Je ne comprends pas où est mon erreur je trouve pas la même chose que vous.

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 19:20

larrech @ 17-09-2018 à 18:59

Bonsoir,

Vous aurez , sauf erreur, r_{n}= r\prod_{k=1}^{n} cos( \dfrac{\theta}{2^k} )

Le calcul du produit est un classique, exprimer chaque terme en fonction du sinus de l'angle double

(en complément de ce qu'a déjà dit Glapion et à seule fin de ne pas avoir écrit ça pour rien)


Pourriez vous m'expliquer comment vous trouvez r_n je me trompe toujours dans ce genre de calcul

Posté par
larrechre : Suite à termes complexes 17-09-18 à 19:34

En cas de doute, on peut se vérifier avec les premiers termes.

Ici z_{1}=r_{1}e^{i \theta_{1}} = \dfrac{r +re^{i \theta}}{2}=r e^{i\frac{\theta}{2}} cos(\frac{\theta}{2})

Donc r_1=rcos(\frac{\theta}{2})

Votre erreur doit venir du début de votre calcul

Posté par
Glapion Moderateurre : Suite à termes complexes 17-09-18 à 19:35

oui à mon avis elle est juste ta formule r_n = r \prod_{k=0}^{n-1} cos( \dfrac{\theta}{2^{k}}}) c'est nous qui avons écris trop vite

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 19:46

Je vois pour z1 mais je comprends pas comment obtenir :

r_{n}= r\prod_{k=1}^{n} cos( \dfrac{\theta}{2^k} )

Ça veut dire que j'ai pas compris comment faire

Posté par
Ramanujanre : Suite à termes complexes 17-09-18 à 19:52

A un moment on a :

r_{n-(n-1)}=r_1= r_0 cos(\dfrac{\theta}{2^0})=r_0 cos(\theta)

Mais ce terme n'apparait pas dans votre formule

Posté par
larrechre : Suite à termes complexes 17-09-18 à 21:08

Il est tout à fait possible que je me trompe, mais si on  écrit

r_1=rcos(\frac{\theta}{2})
r_2=r_1cos(\frac{\theta}{2^2})
.....
r_{n-1}=r_{n-2}cos(\frac{\theta}{2^{n-1}})
r_{n}=r_{n-1}cos(\frac{\theta}{2^{n}})

et qu'on multiplie ces égalités membre à membre, on obtient quoi ?

Posté par
luzakre : Suite à termes complexes 17-09-18 à 23:36

On t'a dit de vérifier pour les premières valeurs !
Si tu fais n=1 dans ta formule

Citation :

Soit : r_n = r \prod_{k=0}^{n-1} cos( \dfrac{\theta}{2^{k}}})

tu trouves quoi ? Est-ce correct ?

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 02:31

Ma formule est fausse mais je comprends pas pourquoi pas le calcul Larrech trouve :

r_1=rcos(\frac{\theta}{2})

Alors qu'avec ma relation de récurrence : r_{n+1}=r_ncos(\frac{\theta}{2^n})

Pour avoir r_1 on fait : r_{0+1}=r_0 cos(\frac{\theta}{2^0})

La relation de récurrence ne serait donc pas valable pour n=0 ? Pourquoi ?

Posté par
Zrunre : Suite à termes complexes 18-09-18 à 07:02

L'erreur est dans la formule de récurrence que tu as trouvé pour \theta_n

Posté par
Zrunre : Suite à termes complexes 18-09-18 à 07:03

Edit: je me suis trompé de suite , c'est dans la relation définissant r_n . Désolé , c'est le matin ^^

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 07:10

@Zrun

Vous êtes sûr ? Je vois pas d'erreur dans mon calcul définissant r_n

Posté par
luzakre : Suite à termes complexes 18-09-18 à 08:18

Citation :

La relation de récurrence ne serait donc pas valable pour n=0 ? Pourquoi ?

Parce que r_0=|z_0|=r\neq r\cos(2^{-0}\theta)=r\cos\theta

Rappel : pour démontrer une formule par récurrence (pas une démonstration par "points de suspension", méthode réservée aux professeurs chevronnés(sic)) il y a trois étapes :
Énoncer la propriété à démontrer
Vérifier pour une valeur initiale
Faire l'hérédité.

Tes points de suspension sont un ersatz de l'hérédité mais aucun des deux autres points (pourtant essentiels) n'est abordé.  

Posté par
larrechre : Suite à termes complexes 18-09-18 à 08:30

luzak bonjour!

Les points de suspension ne sont pas les siens, mais les miens...Ce procédé qui camoufle en effet une récurrence, était enseigné et admis sans réticence autrefois (je ne suis plus tout jeune...), tant la récurrence sous-jacente est évidente.
Le fautif qui doit donc être sévèrement morigéné au nom de la RIGUEUR, ce n'est donc pas lui, mais moi.

Cela dit je n'ai rien voulu faire d'autre que de conforter par un moyen visuel simple, le bien-fondé de la formule que j'avais indiquée.

Bien à toi.

Posté par
luzakre : Suite à termes complexes 18-09-18 à 08:43

Citation :

Alors qu'avec ma relation de récurrence : r_{n+1}=r_ncos(\frac{\theta}{2^n})

C'est faux puisque r_{n+1}=r_n\cos\dfrac{\theta_n}2=r_n\cos\dfrac{\theta}{2^{n+1}}

Posté par
luzakre : Suite à termes complexes 18-09-18 à 12:20

larrech bonjour !
Mon "aparté" professeurs chevronnés te concernait aussi.
il est vrai que tu as (comme je le fais souvent aussi) mis des points de suspension mais je visais ceux de Ramanujan (post de 17/09 à  19:01) qui "auraient pu" être la cause de son erreur.
En fait l'erreur était dans ce que j'ai relevé à 08:43.

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 12:45

luzak @ 18-09-2018 à 08:43

Citation :

Alors qu'avec ma relation de récurrence : r_{n+1}=r_ncos(\frac{\theta}{2^n})

C'est faux puisque r_{n+1}=r_n\cos\dfrac{\theta_n}2=r_n\cos\dfrac{\theta}{2^{n+1}}


Vous avez trouvé mon erreur merci !

Démontrons par récurrence que la propriété P(n) définie pour n \in \N^* par :

r_n = r \prod_{k=1}^n cos (\dfrac{\theta}{2^k})

Initialisation :
Au rang n=1 : r_1 = r \cos\dfrac{\theta}{2} donc P(1) est vraie.

Hérédité:
Soit n \in \N^* supposons que P(n) soit vrai.
r_{n+1}=r_n\cos\dfrac{\theta}{2^{n+1}} =  r \prod_{k=1}^{n} cos (\dfrac{\theta}{2^k}) \cos\dfrac{\theta}{2^{n+1}}

Ainsi : r_{n+1}= r \prod_{k=1}^{n} cos (\dfrac{\theta}{2^k})

Ce qui correspond à P(n+1).

On a montré P(1) et \forall n \in \N^* : P(n) \Rightarrow P(n+1)

Conclusion : \forall n \in \N^* : P(n)

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 13:04

Pour la suite :

sin(2x) = 2 cos(x) sin(x) donc : cos(x) = \dfrac{sin(2x)}{2 sin(x)}

Prenons : x = \dfrac{\theta}{2^k}

Ainsi : cos(\dfrac{\theta}{2^k}) = \dfrac{sin(\dfrac{\theta}{2^{k-1}})}{2 sin(\dfrac{\theta}{2^k})}

Donc par télescopage :

\forall n \in \N^* : r_n = \dfrac{r sin(\theta)}{2^n sin (\dfrac{\theta}{2^n})}

Calculons la limite de r_n :

\lim\limits_{n \rightarrow +\infty} r_n = \lim\limits_{n \rightarrow +\infty} r \times \dfrac {sin (\theta)}{\theta} \times \dfrac{\dfrac{\theta}{2^n}}{sin (\dfrac{\theta}{2^n})}=r \dfrac {sin (\theta)}{\theta}  

Comme \theta_n tend vers 0 alors :

Re(z_n) \rightarrow r \dfrac {sin (\theta)}{\theta}  
Im(z_n) \rightarrow 0

D'après le cours : z_n \rightarrow   r \dfrac {sin (\theta)}{\theta}

Posté par
Glapion Moderateurre : Suite à termes complexes 18-09-18 à 13:04

il te reste à transformer ce produit de cosinus en sin /(2n sin(/2n) ce qui permettra de trouver facilement la limite.

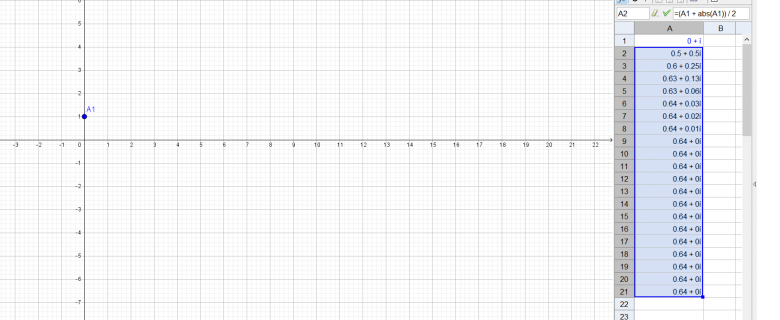
un truc marrant à faire aussi serait dans geogebra d'utiliser le tableur pour lui faire calculer les affixes successives des points et de les visualiser pour vérifier si on trouve bien le même point limite.

Posté par
Glapion Moderateurre : Suite à termes complexes 18-09-18 à 13:07

Je n'avais pas vu ton dernier post. Tu as fini en fait.

Posté par
Glapion Moderateurre : Suite à termes complexes 18-09-18 à 13:14

Suite à termes complexes
geogebra confirme bien, par exemple si on part de z0 = i on atterri bien sur le réel 0.64 qui est bien une approximation de 2/
ça conforte le r sin /

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 13:39

Comment faites vous ça sur Géogebra ? Ca m'intéresse.

Ah vous avez pris \theta = \dfrac{\pi}{2}

Posté par
Glapion Moderateurre : Suite à termes complexes 18-09-18 à 13:49

c'est pas très compliqué :
tu poses un nombre complexe z_0 n'importe où (menu nombre complexe)
tu affiches le tableur de geogebra.
à la première case, la case A1, tu tapes = (z_0+|z_0|)/2
dans la case A2 tu tapes = (A1+|A1|)/2
tu tires la formule vers le bas ce qui calcule automatiquement tous les termes de la suite.
geogebra sans qu'on lui demande, dessine automatiquement les points correspondant dans la zone graphique.

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 15:29

J'ai suivi votre méthode mais ça n'a pas voulu tracer la courbe à part le 1er point

Suite à termes complexes

Posté par
Glapion Moderateurre : Suite à termes complexes 18-09-18 à 15:42

ha bon moi ça crée les points automatiquement, on doit pas avoir les mêmes paramètres.

je crois que c'est dans les propriétés de la sélection (bouton droit propriétés), onglet avancé, la case Localisation Graphique doit être cochée.

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 16:26

Merci bien

Posté par
luzakre : Suite à termes complexes 18-09-18 à 17:41

Pas tout à fait fini car tu as une erreur (que je veux bien prendre pour un lapsus) dans la sommation où tu dis que c'est la propriété pour n+1. La borne supérieure de ta sommation est incorrecte.

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 19:02

Oui luzak je l'ai vue l'erreur juste après avoir posté  mais je sais pas comment modifier un message

Posté par
carpediemre : Suite à termes complexes 18-09-18 à 20:24

salut

luzak :  je ne suis pas d'accord avec toi

larrech @ 17-09-2018 à 21:08

Il est tout à fait possible que je me trompe, mais si on  écrit

r_1=rcos(\frac{\theta}{2})
r_2=r_1cos(\frac{\theta}{2^2})
.....
r_{n-1}=r_{n-2}cos(\frac{\theta}{2^{n-1}})
r_{n}=r_{n-1}cos(\frac{\theta}{2^{n}})

et qu'on multiplie ces égalités membre à membre, on obtient quoi ?
que la relation de récurrence (dernière ligne appliquée à toutes les lignes de 1 à n) soit vraie ou fausse le procédé est tout à fait exact  : il ne fait que multiplier n égalités entre elles  ... indépendamment de leur véracité ...


une dernière remarque :

Ramanujan @ 17-09-2018 à 18:24

z_{n+1}=r_{n+1}e^{i \theta_{n+1}} = \dfrac{r_n +r_{n}e^{i \theta_{n}}}{2}

Donc :

....

Donc : \theta_{n+1} = \dfrac{\theta_n}{2}} et r_{n+1}= r_n cos( \dfrac{\theta_n}{2})    (*)

Ainsi : \theta_{n}  = \theta_{0} (\dfrac{1}{2})^n = \theta (\dfrac{1}{2})^n  

Soit : r_{n+1}= r_n cos(  \theta (\dfrac{1}{2})^n  )

Je vois pas comment calculer r_n
  (*) encore faut-il justifier que r_{n + 1} > 0 puisque c'est sencé être le module de z_{n + 1}

Posté par
Ramanujanre : Suite à termes complexes 18-09-18 à 20:57

@Carpediem

La positivité  provient du fait que r_n est positif par définition et : - \pi \leq \theta < pi

Donc : - \dfrac{\pi}{2} \leq  \dfrac{\theta}{2}< \dfrac{ \pi}{2}

Donc : \forall k \geq 1 :     \dfrac{\theta}{2^k} \in ]-\dfrac{ \pi}{2},\dfrac{ \pi}{2}[

Ainsi :  cos(  \dfrac{\theta}{2^k}) \geq 0

Posté par
carpediemre : Suite à termes complexes 18-09-18 à 21:00

bien sur mais il faut bien le dire ...

Posté par
larrechre : Suite à termes complexes 18-09-18 à 21:16

Ta remarque me réconforte carpediem, merci.

Encore une fois le procédé était jadis couramment employé et nos maîtres d'alors, les Bouteloup, Warusfel et autres, hélas disparus, en remontreraient encore à certains.
Le "chevronné (sic)" te salue amicalement

Posté par
carpediemre : Suite à termes complexes 18-09-18 à 21:56

c'est tout naturel !!

multiplier membre à membre deux ou n égalités est du kif kif au même et on n'écrit jamais ces n égalités qu'on remplace par des petits points ...

bien amicalement

Posté par
luzakre : Suite à termes complexes 18-09-18 à 23:30

Vous ne voulez pas admettre (bon, si mal formulé, je fais mes excuses) que je n'ai rien critiqué : ce genre de choses j'en fais à tout bout de champ.
Je voulais juste inciter Ramanujan à aller voir si  SES points de suspension n'étaient pas cause de son erreur.
En fait, je me trompais, l'erreur venait de son écriture fausse pour \dfrac{\theta_n}2\cdot

Posté par
carpediemre : Suite à termes complexes 18-09-18 à 23:35

j'avais aussi lu ton rectificatif ... mais il est vrai qu'entre "tes", "mes" et "ses" points de suspension ben on s'y perd !!


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !