Inscription / Connexion Nouveau Sujet
Tableau de signes.
D'abord, je voulais vous souhaiter une bonne année avant tout.
J'ai un petit soucis concernant cet exercice, si quelqu'un peut me corriger s'il y a erreur. J'ai reproduis le tableau pour que vous puissiez prendre connaissance de celui ci.
Voici le tableau de signes d'une expression.
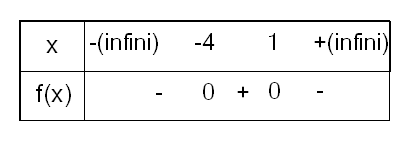
Pour chaque affirmation, dire si elle est exacte.
a) f(-7,5) < 0
b) f( pie)
pie)  0.
0.
c) -4 et 1 sont les solutions de l'équation f(x) = 0
d) Les solutions de l(inéquation f(x)  0 sont les nombres réels de ]-
0 sont les nombres réels de ]- ;-4] ou de [1;+
;-4] ou de [1;+ [
[
e) Les nombres tels que f(x) > 0 sont les réels x vérifiant -4  x
x  1.
1.
Voici mes réponses. f(x) est sur la ligne x, pas vrai ? J'ai un doute. Mes réponses correspondent à la lecture que j'ai faite.
a)Faux
b)  = 3.14. Donc Vrai.
= 3.14. Donc Vrai.
c ) Vrai.
d) Faux.
e) Je ne comprends pas cette affirmation.
Je ne sais pas si je dois justifier, ce n'est pas écrit dans l'exercice.
Merci par avance de votre aide.
Bonjour,
Je crois que tu as un petit problème de lecture d'un tableau.
Le a) est vrai puisque si x = -7,5, tu vois dans le tableau un signe "-" pour f(x).
Donc f(-7,5) < 0
Je ne comprends pas ce que tu as voulu écrire au b).
OK pour le c)
Le d) est vrai car...
Le e) est faux car...
Pour le b), c'est le nombre pie à vrai dire.
J'ai compris : pour le c), f(x)  0 , c'est le -, d'où ]-
0 , c'est le -, d'où ]- ;-4] ou de [1;+
;-4] ou de [1;+ [
[
& pour le d), f(x) > 0 c'est donc le +, d'où dans le tableau, l'intervalle -4  x
x  1.
1.
C'est correct ? Merci pour ton aide Hiphigenie.
Pour le b), tu regardes la position que prend 
 3,14 dans la ligne de x.
3,14 dans la ligne de x.
Tu regardes le signe correspondant pour f(x).
Qu'en conclus-tu ? Le b) est-il correct ?
Pour le e), il faut faire attention. Il est bien marqué f(x) > 0.
Il n'est pas marqué f(x)  0.
0.
Donc -4 < x < 1.
Comme il ne faut pas prendre -4, ni 1, le e) est faux.
Je conclus que f( ) est négatif, donc l'affirmation est fausse, comme f(
) est négatif, donc l'affirmation est fausse, comme f( )
) 0 (sinon il serait positif.)
0 (sinon il serait positif.)
Oups pardon, je pense d'être tromper dans les lettres
pour le c), f(x)
 0 , c'est le -, d'où ]-
0 , c'est le -, d'où ]- ;-4] ou de [1;+
;-4] ou de [1;+ [
[
& pour le d), f(x) > 0 c'est donc le +, d'où dans le tableau, l'intervalle -4
 x
x  1.
1.
C'est le d) et ensuite le dernier le e)
pour le d), f(x)
 0 , c'est le -, d'où ]-
0 , c'est le -, d'où ]- ;-4] ou de [1;+
;-4] ou de [1;+ [
[
& pour le e), f(x) > 0 c'est donc le +, d'où dans le tableau, l'intervalle -4
 x
x  1.
1.On est bien d'accord sur les lettres...
OK pour le d)
Mais pour le e) , la proposition est fausse car la proposition correcte est :
e) Les nombres tels que f(x) > 0 sont les réels x vérifiant -4 < x < 1.
Dans la proposition e) ce qui est faux, c'est que cette propositon autorise x à être égal à -4 ou égal à 1.
Or si x = -4 ou si x = 1, on a f(x) = 0.
Comme l'énoncé dit : f(x) > 0, ...
Comprends-tu ?
Oui, je comprends, sinon ce serait pas + mais -. Je ne suis pas sur que je m'exprime clairement.. mais je comprends tout à fait ce que tu veux dire.
Je te remercie pour cet aide précieuse, et te souhaite une bonne continuation.



