Inscription / Connexion Nouveau Sujet
tableau de variation
Bonjour je suis bloqué à un exercice de maths pouvez-vous m'aider ?
Voici l'énoncé:
Soit f la fonction définie sur  par la courbe représentatrice (1) ci-contre:
par la courbe représentatrice (1) ci-contre:
Où j'en suis:
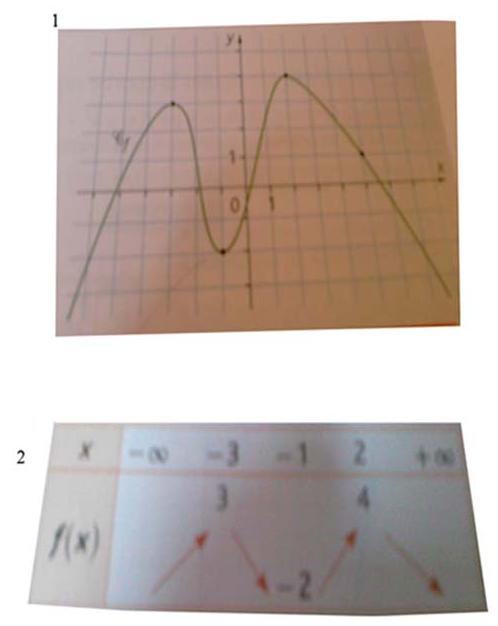
1)dans le corrigé il y a le tableau de variation(2) mais pourquoi est qu'il n'y a pas dans les x 5 et dans les f(x) 1 à la fin du tableau , ça s'arrête à plus l'infinie.
2) comment compte t on le nombre d'image de 0 et le nombre d'antécédent de 0
il y a aussi
3) Lorsque c'est possible comparé:
f(10) et f(15)
où j'en suis:
Dans le corrigé il y a f est décroissante sur l'intervalle [2;+ [, qui contient 10 et 15. Comme 10 < 15, on a f(10)
[, qui contient 10 et 15. Comme 10 < 15, on a f(10)  f(15). est ce que c'est bien ça il n'y a pas d'erreur dans le corrigé ?
f(15). est ce que c'est bien ça il n'y a pas d'erreur dans le corrigé ?
Bonjour ,
un tableau de variation rassemble tout ce qu'on sait sur f(x) quand x varie de - l'infini à + l'infini . Il n'y a pas x=5 bien qu'on connaisse la valeur de f(5) qui est 1 parce que cette valeur 1 n'est pas particulière en ce sens qu'elle ne correspond ni à un maximum ni à un minimum qui seuls permettent de déterminer les parties ou la courbe passe de croissante à décroissante ou inversement .
Pour compter le nombre d'image de 0 , il faut compter combien on a de valeurs différentes pour f(0) .
Pour le nombre d'antécédents , c'est l'inverse : on compte combien de fois f(x) = 0
Ta comparaison entre f(10) et f(15) est correcte et bien justifiée quoique j'aurais écrit f(10) > f(15) plutôt que f(10) >= f(15)
Cordialement
Merci donc si j'ai bien compris:
- Le chiffre 5 dans le tableau de variation qui a comme antécédent 1 ne doit pas être écrit parce qu'il nous indique pas si la courbe est croissante où décroissante (pourtant on dirait que sa baisse à partir de se point).
- Pour compter le nombre d'image de 0, je compte l'ordonné le plus haut que la courbe arrive à atteindre
donc d'après ce que j'ai compris, 0 a pour image 4.
- Pour compter le nombre d'antécédents de 0,je compte combien de fois f(x)=0 c'est à dire le nombre d'abscisses qui est = 0. Donc d'après ce que j'ai compris f(5)=0, 0 a pour antécédent 5.
-Pour la comparaison entre f(10) et f(15) je ne comprend pas pourquoi f(10) f(15) vu que 10 est plus petit que 15 pourquoi 10 serai plus grand ?
f(15) vu que 10 est plus petit que 15 pourquoi 10 serai plus grand ?
Bonjour ,
quelques précisions :
- (pourtant on dirait que sa baisse à partir de se point) Oui mais ça baissait avant et ça baisse après donc rien de particulier .
- nombre d'image de 0 : combien f à de valeurs différentes quand x=0 . Et bien quand x=0 f n'a qu'une seule valeur qui est autour de -0,5
- nombre d'antécédents de 0 : combien de fois f vaut 0 . Et bien le schéma montre que f est égal à 0 quatre fois .
"Donc d'après ce que j'ai compris f(5)=0" non regarde bien la figure : quand x vaut 5 , f ne vaut pas 0 .
- pour la comparaison f(10) avec f(15) je me suis précipité . Il faut remarquer que dans cet intervalle [10;15] la fonction est décroissante (si on extrapole le schéma qui s'arrête à 8 en tenant compte du tableau de variations) . Donc f(10) < f(15)
Cordialement
Encore merci donc si j'ai bien compris:
- pour le chiffre 5 dans le tableau de variation je viens de comprendre
- pour le nombre d'image de 0 si j'ai bien compris il faut regarder par où passe la courbe au niveau de l'axe des ordonnées, la courbe passe seulement par -0.5 et pas ailleurs, donc la seule image de 0 est -0.5. (mais est ce que 0 peut avoir plusieurs images ?)
- pour le nombre d'antécédent de 0 si j'ai bien compris il faut que je regarde par où passe la courbe au niveau de l'axe des abscisse à chaque fois qu'elle y passe, donc elle passe 4 fois sur l'axe des abscisse donc 0 a 4 antécédents.
pour la comparaison entre f(10) avec f(15) pour extrapole tu veut dire (= si on étend la courbe représentative) vu que dix n'est pas sur la courbe représentative. Tu as dis qu'il faut tenir compte du tableau de variation aussi, donc f(10)<f(15) n'a rien à voir avec l'ordre de grandeur des deux nombres mais cela a plutôt un rapport avec la courbe qui baisse autrement dit (qui est décroissante), donc f(10) est situé plus bas que f(15) donc f(10)<f(15).
Pour le nombre d'images et d'antécédents , je pense que tu as compris .
Par contre pour la comparaison , cela me parait encore confus .
Supposons que f(10) = - 6 et f(15) = -9 (valeurs à peu près vraisemblables si on étend la courbe représentative) .
Contre toute apparence -6 > -9 . C'est cela qui t'a trompé je pense . Donc f(10) > f(15) . Ceci est dù effectivement au fait que la courbe est décroissante .

 c'est de ma faute en réécrivant pour la comparaison je voulais mettre f(10) > f(15) et non pas f(10)<f(15).
c'est de ma faute en réécrivant pour la comparaison je voulais mettre f(10) > f(15) et non pas f(10)<f(15).





