Inscription / Connexion Nouveau Sujet
Trigonométrie : deux pivots pour un arc commun
Bonjour, je bloque sur un problème de trigonométrie (enfin je pense) pour une animation 3D qu'on peut résumer de la manière suivante.
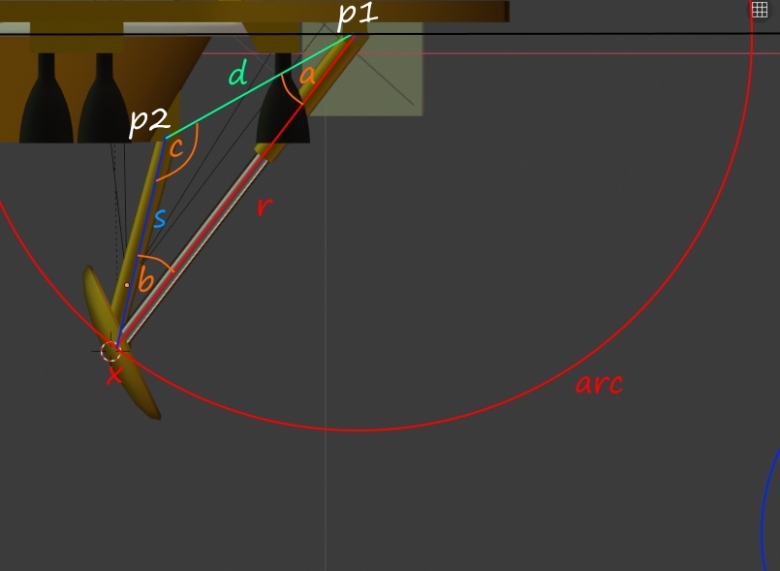
J'ai un mobile composé de deux "bras" r et s. Les points p1 et p2 sont les pivots de chaque bras et sont fixes.
r est fixe.
s est un genre de vérin qui peut donc varier en longueur.
d = 0.340332 m
r = 0.613203 m
r et s se rejoignent en x, et x est toujours situé sur l'arc de cercle de centre p1.
r doit effectuer une rotation de 65° dans le sens inverse des aiguilles d'une montre. En même temps, s doit pivoter sur p2 et s'allonger, en vérifiant les conditions ci-dessus.
Donc j'ai besoin d'une fonction qui fasse varier la vitesse de rotation de s, de manière à r et s restent "attachés" en x. J'avoue que ça me dépasse un peu 
* modération > le niveau a été modifié en fonction du profil renseigné *
L'exercice est compliqué.
Mais en plus, pour l'instant, tu ne sais pas trop ce que tu cherches.
" j'ai besoin d'une fonction qui fasse varier la vitesse de rotation de s .."
Cette question n'est pas claire du tout.
Déjà, une fonction ne fait pas varier une donnée ...
En plus, il n'y avait pas de vitesse jusque là, et maintenant, tu parles de vitesse. Qui dit vitesse dit temps. Et en fait, je pense que la vitesse ne t'intéresse pas. Si le parcours complet se fait en 10 secondes ou en une minute, peu importe.
En fait, commence déjà à bien formuler la question : on dit souvent qu'un problème bien posé est un problème à moitié résolu. Ici, même bien posé, le problème restera compliqué.
Tu peux aussi refaire le dessin, en mettant P1 et P2 sur une même ligne horizontale. Ca ne change pas fondamentalement le problème, et ça peut aider. Du coup , P1 aurait pour coordonnées (0,0) et P2(-0.34,0) , ou encore P1(0.34,0) et P2(0,0)
Ca peut aider à poser des équations plus simples.
Et en fait, je pense que la vitesse ne t'intéresse pas. Si le parcours complet se fait en 10 secondes ou en une minute, peu importe.
Absolument. Le tout est que s et r aient x pour point commun, et que x reste sur l'arc.
Est-ce que ça aiderait si je prends d'autres mesures ? Je pars d'un logiciel de 3D, donc techniquement je peux tout mesurer (même les angles). Je suppose que si je donne les mesures complètes pour la configuration de départ (celle de l'image), ça aide.
Concrètement à l'arrivée je code l'animation en C++, et j'ai, où simdt est "Simulation Delta Time", et sert pour introduire la dimension "temps". anim_proc, c'est le "processus" de l'animation, c'est-à-dire son état : 0 = début, 1 = fin.
double anim_proc;
double da = simdt * 0.1;
// ici le "0.1" détermine la vitesse de l'animation, on a une simple fonction linéaire. C'est ici que j'aurais besoin d'une fonction qui prenne en compte les données du problème.
if (anim_proc < 1.0)
{
ainm_proc = min(1.0, anim_proc + da);
}
Bien sûr à la fin de l'extrait de code j'ai une instruction qui exécute l'animation (appelons-la "animation alpha") :
SetAnimation(anim_alpha, anim_proc);
Le problème, c'est je ne sais toujours pas ce que tu cherches.
Tu as P1 et P2, les emplacements de ces 2 points sont connus. Ok
d , c'est la distance entre ces 2 points, elle est connue. Ok
Tu dis que tu as une situation de départ, celle de l'image. Ok. Donc tu peux mesurer a, b , c et même s ... au choix. On n'aura sûrement pas besoin de tout ça. Si tu mesures a une de ces 4 valeurs, il y a des formules pour trouver les 3 autres.
Ensuite, le point x va se déplacer, sur l'arc de cercle que tu as dessiné.
Ok.
Mais tu veux quoi comme formule ?
Tu veux une formule qui dirait : quand s vaut .... alors c vaut ... Autrement dit, dans le jargon des matheux, la fonction c=c(s) ?
Ou bien une formule qui dirait : quand a vaut ... alors s vaut ..., c'est à dire la fonction s=s(a) ?
Ou bien autre chose encore ?
Alors ce dont j'ai exactement besoin, c'est d'ajuster la vitesse de rotation de s (autour de p2), de manière à ce que pour toute rotation de r (autour de p1) les rotations soient "synchronisées".
Donc pour un angle "alpha" de la rotation de r autour de p1, sachant qu'au maximum cet angle sera de 65° par rapport à la position initiale (dans le sens inverse des aiguilles d'une montre),
Quel doit être (le facteur de) l'angle de la rotation s de pivot p2, de manière à ce que, dans tous les cas, s et r se rejoignent en x ?
On doit obtenir une fonction qui ajuste cet angle au cours du processus de l'animation (0 est le début de l'animation, angle de rotation de r = 0° ; 1 est la fin de l'animation, angle de rotation de r = 65°).
Ok.
Donc la direction ds 2 axes est pilotée par un moteur, la longueur de s s'ajuste toute seule.
Et tu veux que le bras s soit bien orienté dans la bonne direction, quand on impose une certaine direction au bras r. Tu cherches c=c(a)
Dans un triangle, on a les relations sin(c)/r=sin(b)/d = sin(a)/s
Ici, s est inconnu, donc le dernier terme ne va pas vraiment nous aider.
On a donc sin(c)/r=sin(b)/d , et avec quelques manipulations, on arrive (sauf erreur) à :


 en post-bac
en post-bac