Avec 3 curseurs (GeoGebra) , on positionne la courbe comme on la souhaite . Et on dispose de son équation sans calculs .

Bonsoir fm_31,
A mon avis, la question ne consiste pas à trouver une courbe, parmi une infinité, qui corresponde à ce que l'on a envie de démontrer, mais de trouver la courbe qui a le plus de chances de correspondre au phénomène observé.
Bien-sûr, on peut trouver des méthodes visuelles et intuitives, mais autant utiliser des méthodes plus rigoureuses.  

Voici ce que donne une régression par une exponentielle...
C'est très proche... avec un léger avantage à l'exponentielle sur le mois 1.
Les coefficients sont plus stables.
Si les deux mois concernent le même équipement, on peut éventuellement superposer les deux nuages et régresser globalement.

Premier mois :



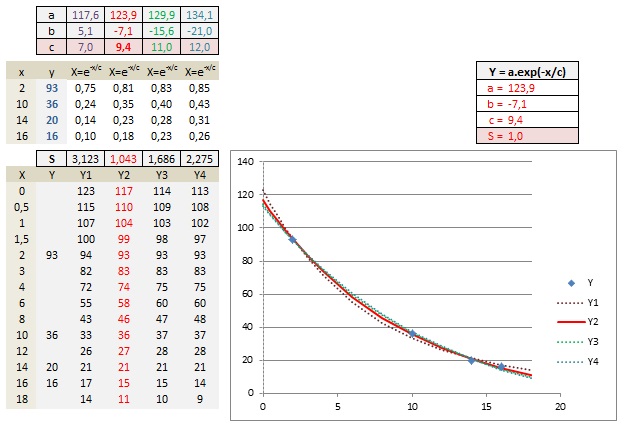
Deuxième mois :

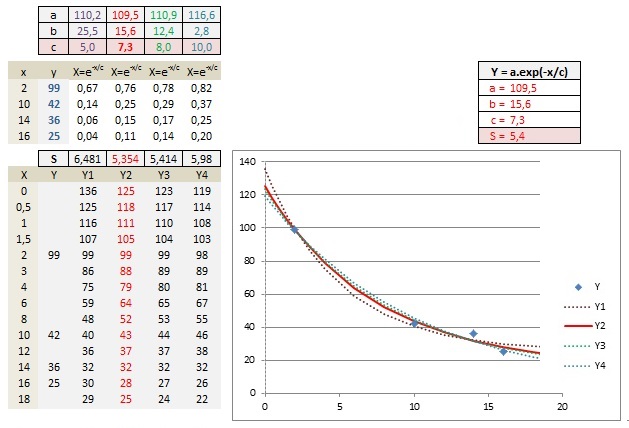
... et en superposant les points de M1 et M2...
Les deux modèle (HYP) et (EXP) sont très proches...
les paramètres de l'hyperbole sont plus "parlants"...

Modèle Hyperbole :



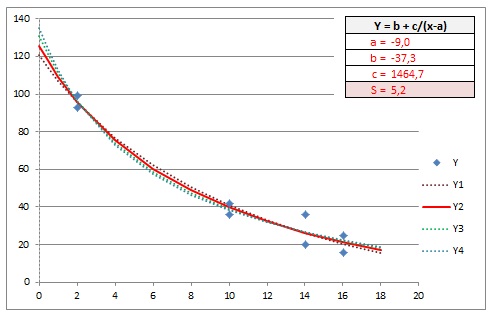
Modèle Exponentielle :

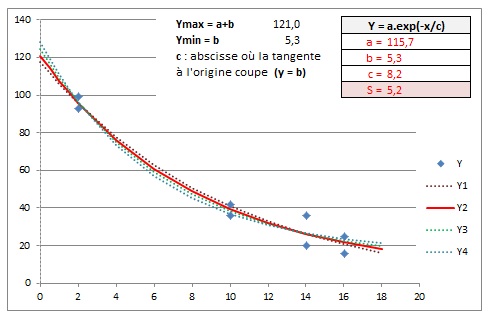
@ LeDino  

bonjour,
je vois que le model de LeDino est plus proche de ce que j cherche,je parle du model de Y=b+c(X-a),
j veux juste savoir comment suivre pour avoir ces resultats sur excel, comment vous proceder pour varier le a et comment faire pour tracer et afficher l'equation
merci de votre compréhension

comment calculer l'erreur quardiatique et pourquoi faire?c est quoi son role?

Bonsoir mariamaaa,

Désolé de ne pas t'avoir répondu plus tôt : manque de temps...

Ton problème correspond à ce qu'on appelle une régression non linéaire.
Tu as un "nuage de points" définis par leurs coordonnées .
Ce nuage a une forme particulière que tu cherches à modéliser par une expression que tu conjectures grâce à des hypothèses sur le comportement du système que tu observes (et qui permettent de cerner la relation entre les grandeurs X et Y...), ou simplement de façon empirique (mon nuage "ressemble à une hyperbole"...).

Dans ce cas, tu vas écrire :  ,  où est une estimation de Y.
En général, F(X) dépend de paramètres (a, b, c...).
Le but de la régression est de trouver les paramètres (a,b,c...) qui ajustent au mieux le nuage de point.

Pour mesurer la qualité de cet ajustement:  on applique le plus souvent le critère des "moindres carrés".
Il s'agit tout simplement de la somme des carrés des écarts entre les    et les  


NB : Minimiser ce critère revient aussi à minimiser "l'erreur quadratique moyenne" :  

Le cas le plus simple : la régression linéaire
Si F(X) est de la forme  Y = aX + b  ... on fait une régression linéaire.
Dans ce cas, le calcul des paramètres de l'optimum (minimum d'erreur) s'obtient simplement par des formules directes).
Tu peux obtenir les paramètres avec EXCEL grâce aux fonctions :
DOITE.REGRESSION (pour obtenir la pente a)
et ORDONNEE.ORIGINE (pour obtenir b).

Autres cas simplifiables : linéarisation
Si F(X) n'est pas une fonction linéaire, on peut parfois s'arranger néanmoins pour transformer X et Y en X' et Y' tels que la relation entre ces variables transformées soit linéaire.

Exemple :  
On pose :  
Il vient :  

On peut alors obtenir    et    par la régression linéaire.

Le cas général :
Si F(X) n'est pas linéaire, ni linéarisable...
Alors la méthode consiste à faire une recherche du minimum de la fonction d'erreur SCE calculée sur les points du nuage.
SCE dépend des paramètres a,b,c...
En général, les outils spécialisés requièrent l'expression des dérivées partielles de F par rapport aux paramètres a,b,c...
Elles demandent également une "grille" de valeurs de départ des paramètres, pour quadriller l'espace des paramètres et minimiser les risques de "passer à coté" de la valeur minimale...


Ton cas à toi est intermédiaire :  F(X) est en partie linéarisable.
On peut alors trouver facilement b et c par régression linéaire.
A condition de fixer a.
Donc l'idée consiste à faire varier a, et à calculer b et c par régression linéaire.
On regarde l'erreur type S.
Quand elle est minimale : on a trouvé la solution du problème.

... la suite plus tard ...

Donc dans le cas où tu poses :  

... tu as une fonction hyperbolique (donc non linéaire),
... cette fonction est en partie linéarisable, mais pas totalement.

En effet, on peut la réécrire :     avec  

Donc si    est fixé, on peut obtenir    et    simplement par régression linéaire.
Une méthode simple pour toi peut consister à faire varier    par toi même ("à la main"), en resserrant peu à peu la plage de valeurs qui rend l'erreur S minimale.
En quelques itérations manuelles on trouve très vite la solution.

Il y a des méthodes pour faire faire ce travail par l'ordinateur, mais les maîtriser demande un petit investissement, qui n'est pas forcément justifié ici...

Sur tableur, la solution "à la main" ressemble à ceci :



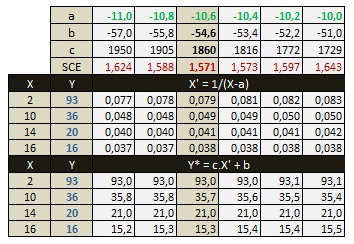
La colonne  a = -10,6  correspond au minimum de SCE (somme des carrés des écarts).

Formule pour b (1ère colonne) :  D4 = ORDONNEE.ORIGINE($C$8:$C$11 ; D8: D11)
Formule pour c (1ère colonne) :  D5 = DROITEREG($C$8:$C$11 ; D8: D11;VRAI)
Formule de SCE (1ère colonne) :  D6 = SOMME.XMY2($C$13:$C$16 ; D$13: D$16)

SOMME.XMY2  donne la somme des carrés des écarts entre deux plages de valeurs.

bonjour
désolée pour le retard,
je viens de terminer cette étude j ai essayer de faire a peut prêt la même démarche de LeDino
et j ai eu enfin ma fonction hyperbole
merci à vous tous