Bonjour,

Une idée...

Soit n et p les paramètres de la loi.

CasFavorables = 0
Répète 1000 fois ce qui suit
[DEBUT]
Tire n fois au hasard un nombre réel dans [0;1].
Compte le nombre de fois où le nombre est <= à p. C'est le nombre de succès.
Si ce nombre est dans [A;B], incrémente casFavorables de 1
[FIN]
Puis divise casFavorables par 1000.
Tu obtiens une approximation de la probabilité souhaitée.

Nicolas

Par exemple, prenons :
n = 400
p = 0,45
[A;B] = [180;200]

En utilisant la fonction LOI.BINOMIALE d'Excel, on trouve 0,47778841 comme approximation de la probabilité cherchée.

Ci-dessous un programme possible sous Algobox.
Mais je me méfie de la fonction random() de ce logiciel.

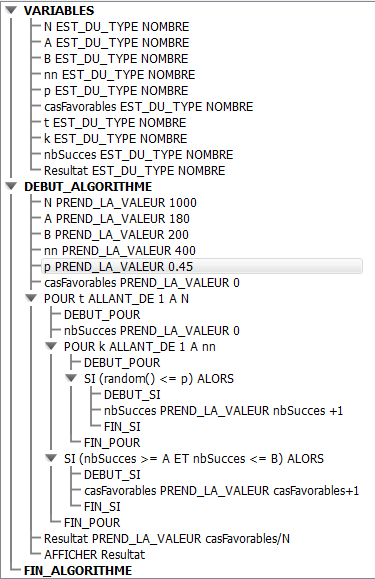
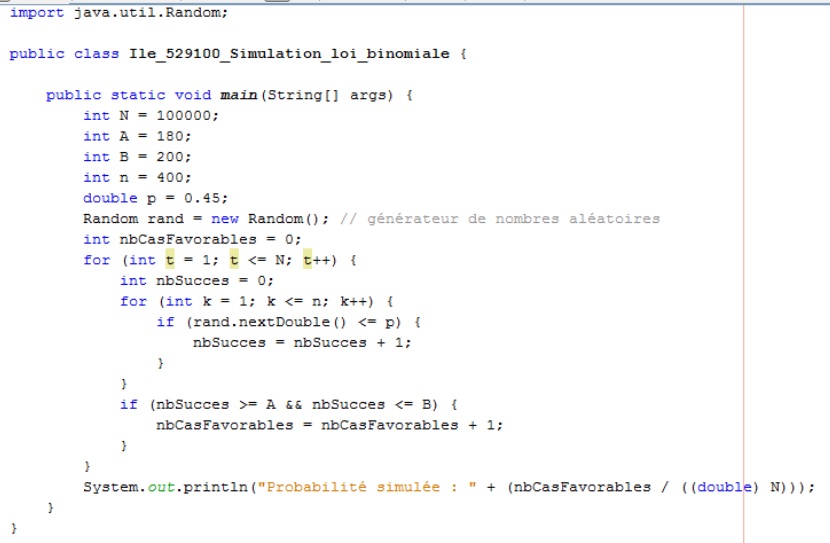
Ci-dessous un programme possible sous Java.

Je l'ai essayé trois fois, et ai obtenu successivement :
0,49981
0,50026
0,49869

Correction d'un message ci-dessus :

En utilisant la fonction LOI.BINOMIALE d'Excel, on trouve 0,49949 comme approximation de la probabilité cherchée.

Enfin, on peut vérifier l'approximation par une loi normale.

On sait que :

où suit la loi normale d'espérance et de variance ().

Si suit une loi normale centrée réduite, on a donc :






En regardant dans les tables ou en utilisant la fonction LOI.NORMALE.STANDARD d'Excel, on trouve 0.4778 comme approximation de la probabilité cherchée.

Sauf erreur.

Nicolas