Inscription / Connexion Nouveau Sujet
Union de rectangles de R2
Bonsoir, je suis actuellement en train de travailler sur un devoir maison mais je n'arrive pas à traiter correctement une question.
Avant tout un peu de matériel, on appelle rectangle de R2 un compact de la forme [a,b]x[c,d] avec a,b,c,d des réels et on dit que A appartient à Rect<infini ssi il existe R1,_,Rn rectangles 2 à 2 disjoints A = Union pour j allant de 1 à n des Rj.
Il faut que je montre que l'application F : Rect<infini -> R+
A |-> somme pour j allant de 1 à n de F(Rj)
est bien définie. (A peut être plusieurs union de rectangle différents, il n'y a pas unicité)
Il faut donc montrer que si A = Union pour j =<n des Rj = Union pour k =<m des Rm alors somme pour j allant de 1 à n de F(Rj) = somme pour k allant de 1 à m de F(Sk)
(Désolé de ne pas utiliser latex....)
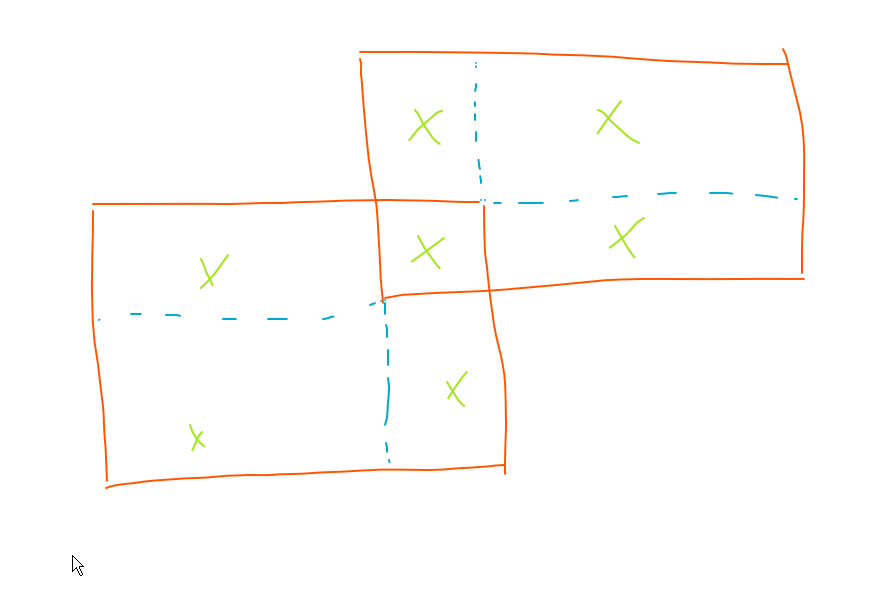
J'ai essayé de raisonner sur seulement deux rectangles A et B de Rect<infini (image) qui ne sont pas 2 à 2 disjoints, on les découpe ensuite en plusieurs rectangles et finalement on voit que l'aire est là même quelque soit le découpage, mais je vois pas du tout comment le démontrer proprement...
Pourriez-vous m'aider ?
Bonjour
Peut-être qu'en sachant ce que désigne F pour les rectangles ordinaires, on serait plus à même de t'aider ?
Si j'ai bien compris ton " Rect<infini " est défini ainsi :
A 
" Rect<infini " SSI il existe n 
* et R1,....,Rn des rectangles compacts de 
² tels que Rj 
Rk = 
si j 
k et tels que A soit leur réunion .
Le dessin que tu fais ne correspond pas à cette définition .
Il me semble que si A " Rect<infini " et si (R1,....,Rp) , (U1,....,Uq) sont 2 telles décompositions de A
alors p = q et il existe u Sn telle que Uk = Ru(k) pour tout k .
On n'a qu'à considérer la relation G sur A définie par : (x G y) SSI [x , y] 
A qui est une équivalence .
Autrement dit " Rect<infini "est formé des part ies A de ² dont les composantes connexes sont des rectangles compacts en nombre fini .
Le dessin qu'il fait peut correspondre si on entend par «disjoints» «d'interieurs disjoints». L'énoncé a définitivement besoin d'être précisé
Bonjour
Peut-être qu'en sachant ce que désigne F pour les rectangles ordinaires, on serait plus à même de t'aider ?
Bonjour, oui désolé j'ai oublié de mentionner F
En fait F( [a,b]x[c,d]) = max{0,(b-a)*(d-c)}
Si j'ai bien compris ton " Rect<infini " est défini ainsi :
A
" Rect<infini " SSI il existe n * et R1,....,Rn des rectangles compacts de ² tels que Rj Rk = si j k et tels que A soit leur réunion .
Le dessin que tu fais ne correspond pas à cette définition .
Il me semble que si A
" Rect<infini " et si (R1,....,Rp) , (U1,....,Uq) sont 2 telles décompositions de A
alors p = q et il existe u
Sn telle que Uk = Ru(k) pour tout k .
On n'a qu'à considérer la relation G sur A définie par : (x G y) SSI [x , y]
A qui est une équivalence .
Autrement dit " Rect<infini "est formé des part ies A de
² dont les composantes connexes sont des rectangles compacts en nombre fini .
Oui mon dessin est faux en fait j'ai mal comprit l'énoncé et j'ai voulu m'illustrer ça avec A et B deux élément de Rect<infini composés tous les deux d'un seul rectangle mais ça n'a rien à voir en fait...
Il me semble que si A
" Rect<infini " et si (R1,....,Rp) , (U1,....,Uq) sont 2 telles décompositions de A
alors p = q et il existe u
Sn telle que Uk = Ru(k) pour tout k .
Donc on prend A
" Rect<infini " sur mon dessin je dis que A c'est l'union de R1 et de R2 mais aussi de S1,...,S5
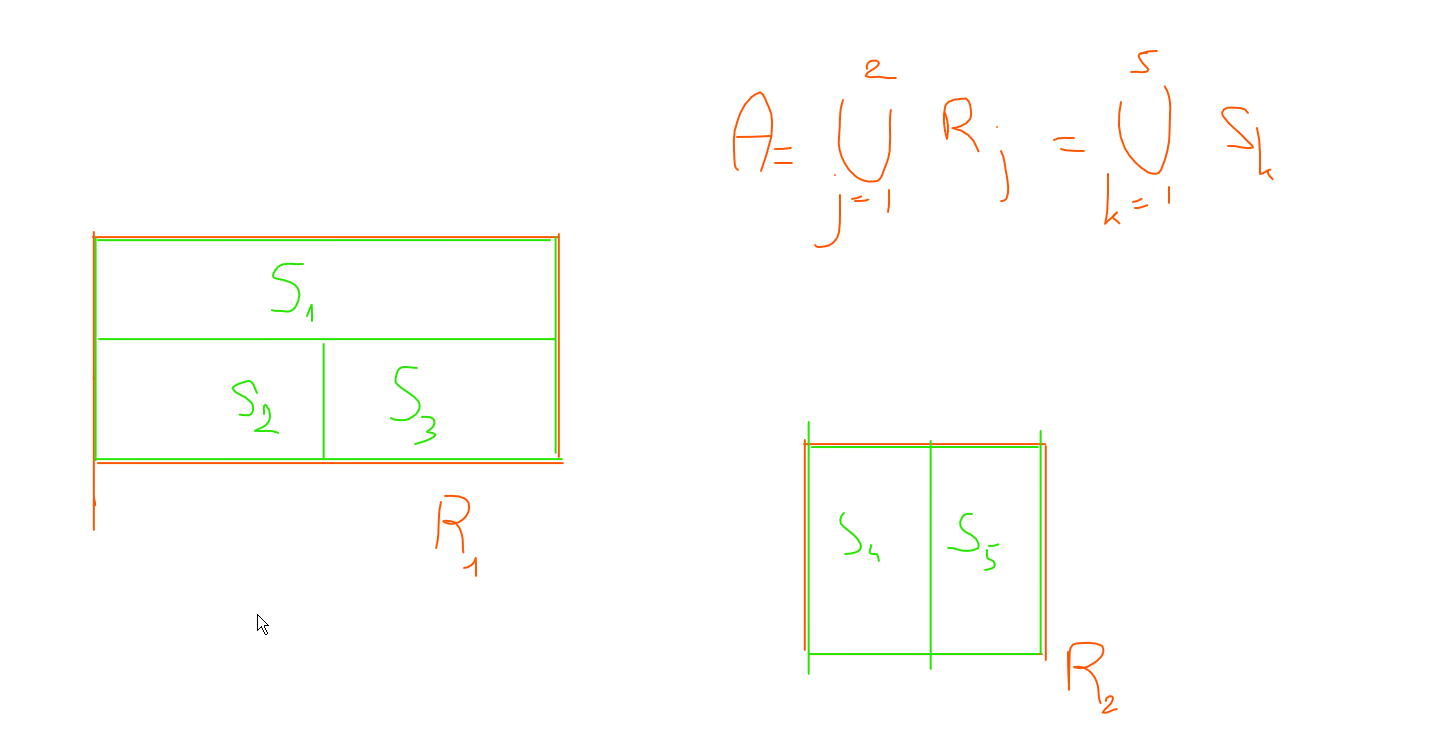
Maintenant que j'ai découpé R1 et R2 en plusieurs autres rectangles, j'ai calculé F(R1) = max{0,(b-a)*(d-c)} = ac -ad -bc + bd et ensuite j'ai calculé F(S1)+F(S2)+F(S3) = max{0,(b-a)*(d-c)/2} + max{0,(b-a)/2*(d-c)/2} + max{0,(b-a)/2*(d-c)/2}= ac -ad -bc + bd
On fait pareil avec R2 et on trouve que F(R2)=F(S4)+F(S5)
Donc là avec ce découpage précis ça marche bien mais je ne vois pas du tout comment je pourrais démontrer cela correctement pour n'importe quel découpage
ça ne va toujours pas !
Un rectangle fermé ne peut pas être réunion de 2 rectangles fermés disjoints .
Désolé mais je comprends pas vraiment ce que tu me dis, j'ai bien prit A une union de deux rectangles disjoints et ces deux rectangles R1 et R2 je les ai bien découpé en d'autres rectangles Sk plus petits
Ou alors je ne comprends pas l'énoncé
je ne comprends pas comment (b-a)(d-c) peut être autrement que positif ? et F représenterait juste l'aire du rectangle , non ?
tu es certain qu'il n'y a pas le mot "intérieur" devant "disjoint" dans la description de ton Rect
Bonjour.
Cet exercice ressemble fort à une introduction au théorème de Fubini.
Mais ce qui est bizarre, c'est que l'on n'a affaire ni à une tribu, ni à un clan, ni à une classe monotone.
A mon sens, il faut considérer les rectangles au sens le plus large, savoir de la forme où la barre verticale est indifféremment un crochet à droite ou à gauche, la mesure du bord étant nulle par définition. Dans ce cas, on peux faire toutes les superpositions que l'on souhaite.
je ne comprends pas comment (b-a)(d-c) peut être autrement que positif ? et F représenterait juste l'aire du rectangle
tu es certain qu'il n'y a pas le mot "intérieur" devant "disjoint" dans la description de ton Rect<Infini ?
encore une fois, peut on avoir un énoncé complet et précis, au mot près ?
Alors la définition exacte que j'ai sur mon énoncé c'est : Le mot rectangle désigne un compact de la forme [a,b]x[c,d] avec a,b,c,d
, attention rien n'obligé b à être supérieur à a ! En particulier si b<a ou d<c, alors [a,b]x[c,d]=
une partie K
x est compacte lorsqu'elle est fermée et bornée
et encore on définit l'ensemble Rect<infini dont les éléments sont les unions finies et disjointes de rectangles
A
Rect<infini 
A=
Rj avec R1,_,Rn des rectangles 2 à 2 disjoints
Bonjour.
Cet exercice ressemble fort à une introduction au théorème de Fubini.
Mais ce qui est bizarre, c'est que l'on n'a affaire ni à une tribu, ni à un clan, ni à une classe monotone.
A mon sens, il faut considérer les rectangles au sens le plus large, savoir de la forme
En fait la première question de cette partie était de montrer que l'ensemble Rect<infini est un clan booléen, c'est-à-dire que pour tout A,B
Rect<infini A
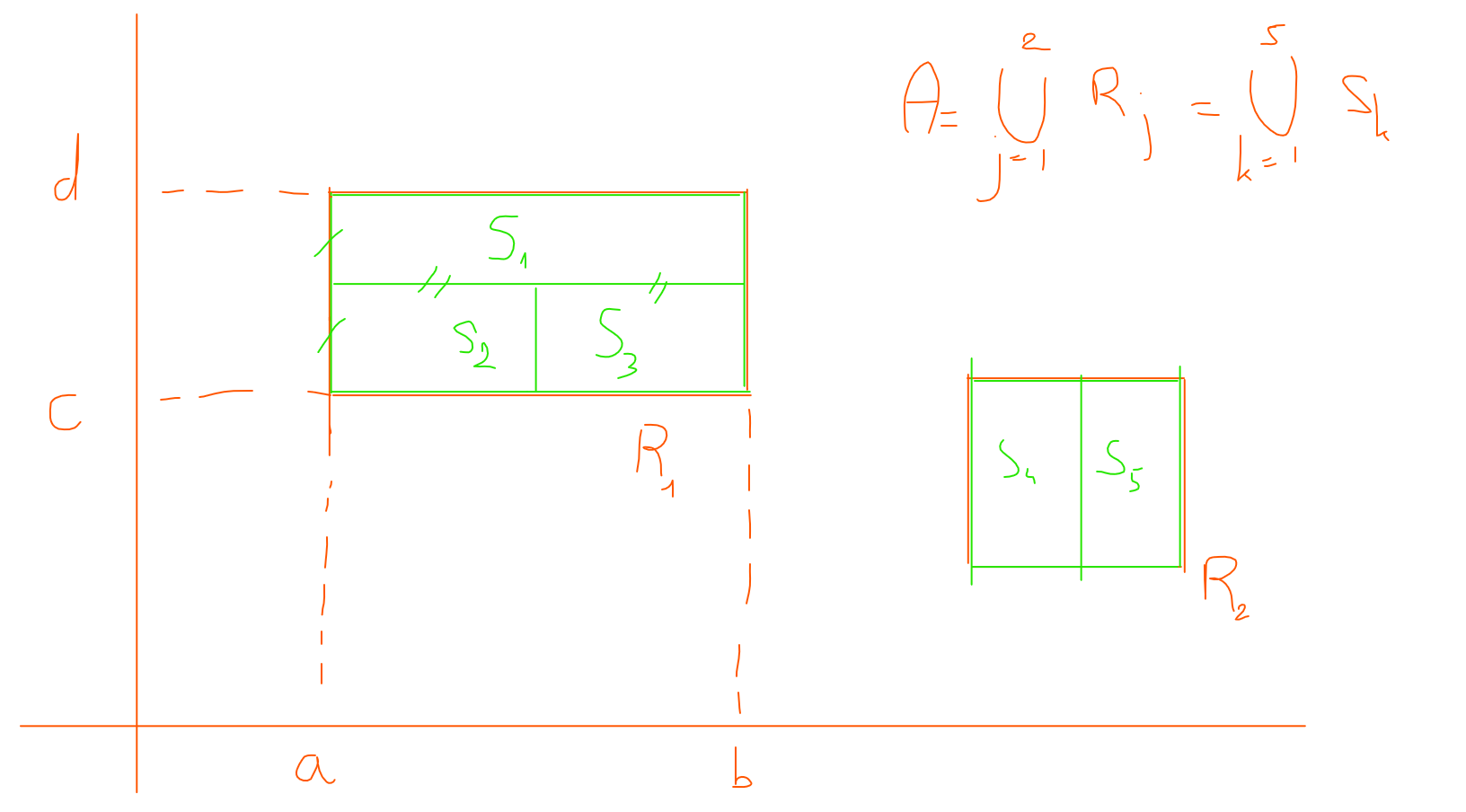
BRect<infini et A\BRect<infiniSur mes 3 figures ici je prends A = Rj mais avec un seul Rj donc A=R
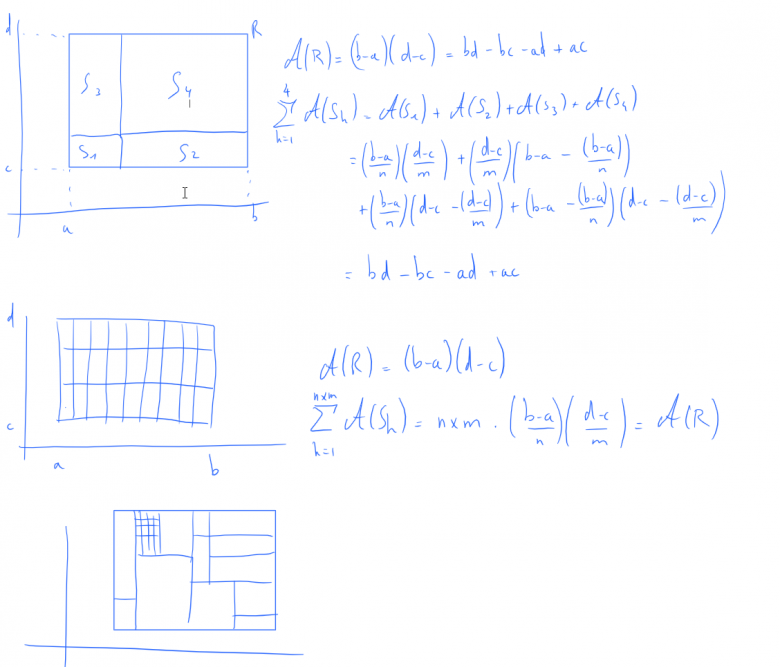
Sur la première figure, j'ai essayé de généraliser la découpe en 4 en m'inspirant de ce que j'avais montré sur mon dernier dessin.
La deuxième figure c'est dans le cas où on a n*m fois le même rectangle.
La troisième figure c'est dans le cas où R est découpé de manière quelconque mais je vois pas quoi faire justement
Si on considère uniquement les rectangles compacts, on n'aura jamais un clan.
Si tu superposes deux rectangles fermés, il est impossible d'écrire la réunion de ces deux rectangles comme réunion disjointe de rectangles fermes.
Prends et
: à qui est attribué le point
?
De plus, comment écrire le complémentaire d'un rectangle compact, qui est non borné, comme union finie de rectangles bornés ?
De plus, comment écrire le complémentaire d'un rectangle compact, qui est non borné, comme union finie de rectangles bornés ?
Mais un rectangle c'est un compact de la forme [a,b]x[c,d] et on dit qu'une partie de R2 est compacte si elle est fermée et bornée
Oui c'est fait!
Je pense qu'il y a clairement un problème d'énoncé.
Prend un unique rectangle. S'il est censé faire partie d'un clan formé d'unions finies de rectangles compacts, alors son complémentaire doit être compact, et évidemment, ce n'est pas le cas.
Donc en gros là, si je prends A et B deux éléments de éléments Rect<infini, ils peuvent être placé comme ça, A\B n'est pas un compact à cause de R2\S2, mais vu que Rect<infini est un clan booléen, A\B devrait être compact, donc on a une contradiction avec l'énoncé ?
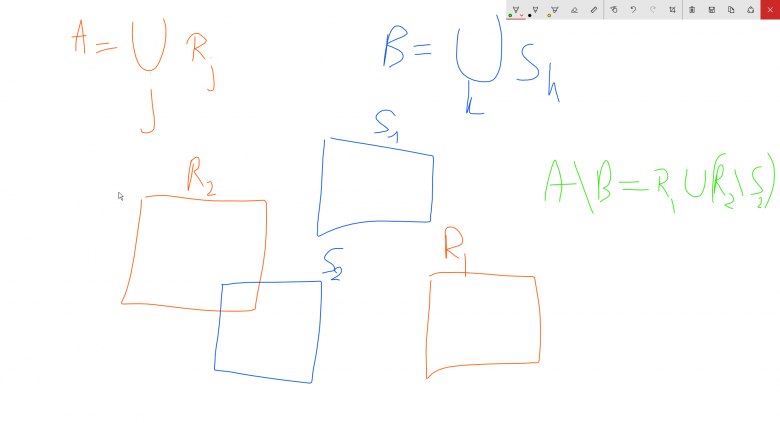
Pour moi il y a une contradiction. mais je vais recopier, comme je l'ai annoncé, l'énoncé pour que les autres puissent donner leur avis
Je remplace "rectangle compact " par "rectangle de la forme [a , b[
[c , d[ " .
Je considère donc
. l'ensemble X formé des [a , b[ [c , d[ où (a,b,c,d) 4 vérifie a 
b et c d (on pose m([a , b[ [c , d[) = (b - a)(c - d) ) ,
. puis l'ensemble Y formé des réunions finies disjointes d'éléments de X .
Il est clair que X Y .
Soit A Y .
Si G := (Rj)jJ est une famille d'éléments disjoints de X on pose m(A,G) = 
{ m(Rj) | j J } .
Il se peut qu'il existe une d' autres" famille disjointes " de Y dont A soit la réunion .
On montre alors qu'on a : (*) { m(A,H) | H est une " famille disjointes " de Y dont A est la réunion } est un singleton ( qu'on peut noter m'(A))
Comme dans le cas où A X on a m'(A) = m(A) cette notation m ' est abandonnée .
Voila pour le "bien défini " de m(A) .
Ceci permet de prolonger m à Y de telle sorte que si A et B sont dans Y et A B = on ait m(AuB) = m(A) + m(B) .
Pour montrer (*) il suffit de montrer que si A X et (Rj)jJ est une " famille disjointe " de Y de réunion A alors m(A) = j m(Rj) .
La , pour t'aider , tu peux faire des dessins du type du dernier de ceux que tu as fait hier à 17:35 .
En prolongeant les coté de tous le rectangles contenus dans A ( le gros ) tu obtiens une nouvelle partition K de A par des éléments de X .
Annuler
connectez vous
analyse en post-bac