Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
volume d'un tétraèdre
Posté par skendaou
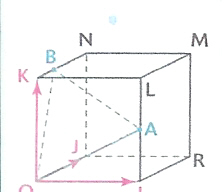
L'espace est muni d'un repère orthonormal (O; OI, OJ, OK) et on considère le cube OIRJNKLM.
A est le milieu de l'arrète [IL] et B est le point défini par: KB=(2/3)KN.
On note P le plan (OAB).
1.a) Préciser les coordonnées des points A et B.
b) Calculer le volume du tétraèdre OABK.
2. a) Déterminer une équation du plan P.
b) Calculer la distance du point K au plan P.
c) En déduire l'aire du triangle OAB.
Alors pour la 1.a) j'ai trouvé A(1,0,0.5) B(0,2/3,1)
pour la 2.a) j'ai trouvé (P): x+3y-2z=0 pour n(1,3,-2)
j'aimerais savoir si mes résultats sont justes pour le moment svp?? merci d'avance pour votre aide
BONJOUR QUAND MEME!
Oui, tout est juste.
Pour la question 1b), choisis pour base OKB, c'est le plus simple.
merci!
mais est-ce que vous pouvez me rappeler la formule du volume d'un tétraèdre parce que je ne la connais pas svp??
encore merci
re bonjour! excusez moi je n'arrive pas à trouver la hauteur h du tétraèdre OABK parcontre pour la base OBK j'ai trouvé B=
13/6 mais je ne sais pas si c'est juste.
merci d'avance
Avec plaisir.
Le volume d'un tétraèdre, c'est [(aire de la base) x (hauteur relative à cette base)/3].
La hauteur relative à cette base est l'unique droite passant par A et orthogonale au plan (OKB)...réfléchis, c'est assez immédiat!
Enfin je ne comprends pas ton calcul d'aire de la base, il s'agit tout bonnement de l'aire d'un triangle, rectangle en B qui plus est: la réponse est 1/3.
excusez moi je ne comprend pas comment vous faites pour trouver 1/3 je trouve toujours une racine carré.
c'est bien B=(KB*OB)/2 non?
ah voilà c'était ce que j'avais fait au début mais j'ai cru que je m'étais trompé merci!
mais je trouve pour ||KB||=2/3 et pour ||KO||=1
c'est pour ça que je trouve
(13)/6
Non, la hauteur doit être orthogonale à toute droite du plan de base:
or (OA) n'est pas orthogonale à (OK) par exemple.
Toujours pas, (AK) est-elle perpendiculaire à chaque droite de (OKB) ??
N'aie pas peur d'introduire un point supplémentaire sur la figure!
et comment je fais alors pour calculer cette hauteur??
Je prend par exemple en appelant G un point de la droite OK et je calcule GA c'est ça?
Bon il faut une droite passant par A et perpendiculaire à (OK) déjà...
Tu n'en vois pas une évidente?(Encore une fois, il faut introduire un point supplémentaire!)
je ne comprend pas il faut reprendre un point du cube,faire un projeté?
je pensé qu'il fallait introduire un point quelconque
mais par contre pour la dernière question je n'ai pas trop compris comment je devais faire! déjà j'ai trouvé K=(14)/7 c'est ça?
Merci
Oui, je trouve ça aussi.
En appelant d cette distance, et H le projeté de K sur le plan (OAB), on obtient un deuxième moyen de calculer le volume du tétraèdre:
d.aire(OAB)/3.
Comme ce volume est connu (question 1b) et que d est connu, on peut en déduire l'aire de OAB facilement.
Je trouve pour aire: , ou encore
.
si ça vous dérange pas de m'aider encore un peu, j'ai un autre exercice mais sur la méthode de Gauss je dois résoudre un système à 4 lignes et je sais pas comment on fait?? 