j'ai oublié dans l'équation de multiplier par un sinus :


int( sin*sin( sum( puissances de sinus ) ) )

C'est d'autant plus drole.

L'écriture de votre question est trop ambigue.
Il faudrait que les fonctions soient clairement définies, par exemple écrire sin(x) au lieu de sin , de façon à ce qu'on sache de quel argument il s'agit.
Il faudrait aussi écrire quel est l'élément différentiel dans l'intégrale, par exemple dx, de façon à savoir par rapport à quoi l'intégration est demandée. Sans ces indications, l'écriture n'a pas de sens bien défini et se prète à des interprétations multiples.

  Bien, je recommence:

c'est ce genre d'intégrales qui m'intéressent:

int( sin(x)*sin( sum ( a*sin(x)+b*sin(x)^2+c*... ) ) dx)
avec a, b, c... réels

ou, mais c'est pareil :
int( cos(x)*sin( sum ( a*sin(x)+b*sin(x)^2+c*... ) ) dx)
  
Voila. Dans la somme, si l'ordre du polynome de sinus est 1, la solution se trouve en fonction de fonctions de Bessel, si elle est de deux, il y a surement un moyen de s'arranger avec des integrales de Fresnel...

Pour les fonctions du genre:
sin(x)*sin(a*(sin(x))^n)
et cos(x)*sin(a*(sin(x))^n)
on sait comment exprimer leurs primitives avec des fonctions de Bessel, de Fresnel, ou de Boehmer, suivant les cas.
Lorsqu'il y a plusieurs termes en puissances de sin, comme pour les fonctions :
sin(x)*sin(a*sin(x)+b*(sin(x))^2)+c*(sin(x))^3+...)
on peut, théoriquement, se ramener à une somme de fonctions, chacune du genre suivant :
sin(x)*sin(A*sin(x))*sin(B*sin(2x))*...
(avec cos au lieu de certains sin )
Dans ce cas général d'un produit de plus de deux termes en sin(sin(k.x)) et/ou cos(sin(h.x), je ne connais pas de méthode pour trouver une primitive se ramenant à une ou des fonctions spéciales répertoriées.
Il est possible que l'on puisse se ramener à une ou des fonctions hypergéométriques dans certains cas ne comportant qu'un petit nombre de paramètres. Cela demanderait une recherche plus approfondie.

Note : ma réponse précédente valait pour les primitives, donc pour les intégrales indéfinies.
Par contre, si la question était posée pour l'intégrale définie de x=0 à x=pi, il est évident que le problème serait beaucoup moins général et possibilités de réponses sous forme de fonctions spéciales répertoriées seraient plus étendues.

   Merci, ça me sera très utile.
  Ah, et oui, c'était pour des intégrales définies (de -pi à pi), donc j'ai tout ce qu'il me faut. En fait, pour l'instant, cela me suffit de savoir que c'est possible à résoudre analytiquement (dans une certaine mesure).

  Encore merci

Bonjour,

Le doccument joint répond à votre question dans quelques cas simples.
Dans certains cas plus compliqués, il y a des méthodes pour effectuer l'intégration d'une façon formelle. Lorsque j'aurai un peu plus de temps, je donnerai des indications à ce sujet (cela demande un travail substanciel de mise en forme)

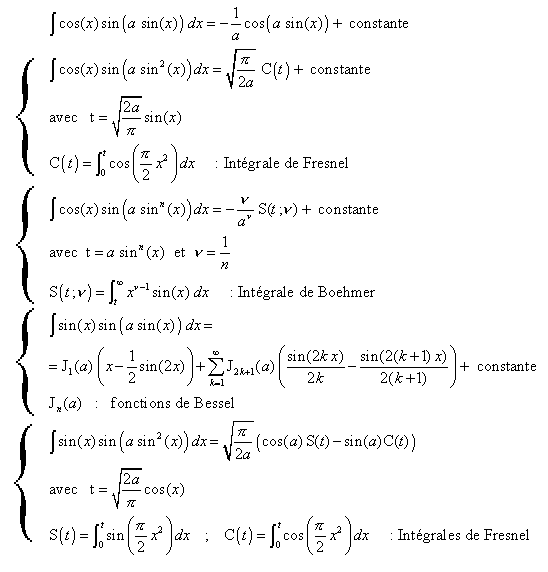
  Encore merci !

  En fait, je suis en train de travailler sur de la spectroscopie par modulation de longueur d'onde, et par la loi de Beer-Lambert, j'en suis arrivé à ces équations. J'ai simulé mes calculs, mais je voulais juste savoir si ils étaient calculables analytiquement pour des études postérieures. En fait, je fais mon projet de fin d'étude (d'ingénieur) dans une entreprise de détecteurs de glace à bas prix en Suède (en bureau d'études), et je vais bientot écrire mon rapport. Je voudrais remercier ceux qui m'ont aidé, dont vous faites partie. Je vous laisse mon adresse mail pour que si cela ne vous dérange pas, je vous cite dans mon rapport. Ecrivez-moi.

thomas_barthoulot@yahoo.fr