Fiche de mathématiques
Ile mathématiques > maths 1ère > Fonctions : généralités
Polynômes : opérations sur les degrés
=(m^2-4)x^3+(m-2)x^2+x-7)
Determiner le degré de P selon les valeurs de m.
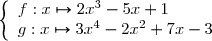
Exprimer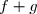 ,
, 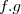 ,
,  ,
, 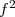 (=
(= 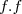 ).
).
f1: x (x - 1)² - 4(2x - 3)(x + 2)² + 3(x - 4)(x + 2)
(x - 1)² - 4(2x - 3)(x + 2)² + 3(x - 4)(x + 2)
f2: x (2x - 1)3 - 2(2x + 3)(x - 4)² - 4(x - 1)²(x + 3)
(2x - 1)3 - 2(2x + 3)(x - 4)² - 4(x - 1)²(x + 3)
f3: x (2x3 + 2x - 1)(4x4 + 5x² + 3).
(2x3 + 2x - 1)(4x4 + 5x² + 3).
P(1) =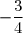 ; P(2) = 1 ; P(3) =
; P(2) = 1 ; P(3) = 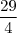 et P(4) = 21.
et P(4) = 21.
![P(x)=(m^2-4)x^3+(m-2)x^2+x-7\\ P(x)=(m-2)(m+2)x^3+(m-2)x^2+x-7\\ P(x)=(m-2)[(m+2)x^3+x^2]+x-7](https://latex.ilemaths.net/latex-0.tex?P(x)=(m^2-4)x^3+(m-2)x^2+x-7\\ P(x)=(m-2)(m+2)x^3+(m-2)x^2+x-7\\ P(x)=(m-2)[(m+2)x^3+x^2]+x-7)
=x-7 )
Le polynôme est de degré 1
=(m-2)x^2+x-7)
Le polynôme est de degré 2
=(m^2-4)x^3+(m-2)x^2+x-7 )
Le polynôme est de degré 3
f(x) = 2x3 - 5x + 1
g(x) = 3x4 - 2x2 + 7x - 3
(f+g)(x) = 3x4 + 2x3 - 2x2 + 2x -2
(fog)(x) = f(g(x)) = 2(3x4 - 2x2 + 7x - 3)3 - 5(3x4 - 2x2 + 7x - 3) + 1
détails du développement de (3x4 - 2x2 + 7x - 3)3
rappel (a+b)3 = a3 + 3a2b + 3ab2 + b3
on peut poser a = 3x4 - 2x2 = x2(3x2 - 2) et b = 7x - 3, ainsi :
(3x4 - 2x2 + 7x - 3)3 = (3x4 - 2x2)3 + 3(3x4 - 2x2)2(7x - 3) + 3(3x4 - 2x2)(7x - 3)2 + (7x - 3)3
détails du développement de (3x4 - 2x2)3
rappel (a-b)3 = a3 - 3a2b + 3ab2 - b3
![(3x^4 - 2x^2)^3 = (x^2(3x^2 - 2))^3 = x^6 (3x^2 - 2)^3 = x^6 [ (3x^2)^3 - 3 (3x^2)^2 \times 2 + 3 (3x^2) \times 2^2 - 2^3] \\\\= x^6 ( 27x^6 - 6 \times 9x^4 + 12 \times 3x^2 - 8) = x^6 ( 27x^6 - 54x^4 + 36x^2 - 8) \\\\= 27x^{12} - 54x^{10} + 36x^8 - 8x^6](https://latex.ilemaths.net/latex-0.tex?(3x^4 - 2x^2)^3 = (x^2(3x^2 - 2))^3 = x^6 (3x^2 - 2)^3 = x^6 [ (3x^2)^3 - 3 (3x^2)^2 \times 2 + 3 (3x^2) \times 2^2 - 2^3] \\\\= x^6 ( 27x^6 - 6 \times 9x^4 + 12 \times 3x^2 - 8) = x^6 ( 27x^6 - 54x^4 + 36x^2 - 8) \\\\= 27x^{12} - 54x^{10} + 36x^8 - 8x^6 )
détails du développement de 3(3x4 - 2x2)2(7x - 3)
![3(3x^4 - 2x^2)^2(7x-3) = 3[x^2(3x^2 - 2)]^2(7x-3) \\\\= 3x^4(3x^2 - 2)^2(7x-3)= 3x^4(9x^4 - 12x^2 + 4)(7x-3) \\\\ = 3x^4 (63x^5 - 27x^4 - 84x^3 + 36x^2 + 28x - 12) \\\\ = 189x^9 - 81x^8 - 252x^7 + 108x^6 + 84x^5 - 36x^4](https://latex.ilemaths.net/latex-0.tex?3(3x^4 - 2x^2)^2(7x-3) = 3[x^2(3x^2 - 2)]^2(7x-3) \\\\= 3x^4(3x^2 - 2)^2(7x-3)= 3x^4(9x^4 - 12x^2 + 4)(7x-3) \\\\ = 3x^4 (63x^5 - 27x^4 - 84x^3 + 36x^2 + 28x - 12) \\\\ = 189x^9 - 81x^8 - 252x^7 + 108x^6 + 84x^5 - 36x^4 )
détails du développement de 3(3x4 - 2x2)(7x - 3)2
(7x-3)^2 = 3x^2(3x^2 - 2)(49x^2 - 42x + 9) \\\\= 3x²(147x^4 - 126x^3 + 27x^2 - 98x^2 + 84x - 18)= 3x²(147x^4 - 126x^3 - 71x^2 + 84x - 18) \\\\= 441x^6 - 378x^5 - 213x^4 + 252x^3 - 54x^2 )
détails du développement de (7x-3)3
^3 = (7x)^3 - 3(7x)^2\times 3 + 3(7x)\times 3^2 - 3^3 \\\\= 343x^3 - 441x^2 + 189x - 27 )
on récapitule le développement de (3x4 - 2x2 + 7x - 3)3

on récapitule le développement de(fog)(x) = f(g(x))
 + 7x - 3)^3 - 5(3x^4 - 2x^2 + 7x - 3) + 1 \\\\= 2(27x^{12} - 54x^{10} + 189x^9 - 45x^8 - 252x^7 + 541x^6 - 294x^5 - 249x^4 + 595x^3 - 495 x^2 + 189x - 27) - 5(3x^4 - 2x^2 + 7x - 3) + 1 \\\\= 54x^{12} - 108x^{10} + 378x^9 - 90x^8 - 504x^7 + 1082x^6 - 588x^5 - 498x^4 + 1190x^3 - 790 x^2 + 378x - 54 - 15x^4 + 10x^2 - 35x + 15 + 1 \\\\ = 54x^{12} - 108x^{10} + 378x^9 - 90x^8 - 504x^7 + 1082x^6 - 588x^5 - 513x^4 + 1190x^3 - 980 x^2 + 343x - 38 )
(2f-3g)(x) = 2f(x) - 3g(x) = 2(2x3 - 5x + 1) - 3(3x4 - 2x3 + 7x - 3) = -9 x4 + 10x3 - 31x + 11
f2(x) = (fof)(x) = f(f(x)) = 2(2x3 - 5x + 1)3 - 5(2x3 - 5x + 1) + 1
détails du développement de 2(2x3 - 5x + 1)3
^3 = (2x^3)^3 + 3(2x^3)(1-5x) + 3(2x^3)(1-5x)^2 + (1-5x)^3 \\\\= 8x^9 + 12x^6 - 60x^7 + 6x^3 - 60x^4 + 150x^5 + (1 - 15x + 75x² - 125x^3) \\\\= 8x^9 - 60x^7 + 12x^6 + 150x^5 - 60x^4 - 119x^3 + 75x^2 - 15x + 1)
d'où
) = 2(8x^9 - 60x^7 + 12x^6 + 150x^5 - 60x^4 - 119x^3 + 75x^2 - 15x + 1) -10x^3 + 25x - 4 \\\\= 16x^9 - 120x^7 + 24x^6 + 300x^5 - 120x^4 - 248x^3 + 150x^2 - 5x - 2)
= x² - 2x + 1 -(8x3 + 32x2 + 32x - 12x2 - 48x - 48)+ (3x2 + 6x - 12x - 24)
= - 8x3 - 16x2 + 8x + 25
polynôme de degré 3
f2(x) = (2x - 1)3 - 2(2x + 3)(x - 4)2 - 4(x - 1)2(x + 3)
rappel : (a-b)3 = a3 - 3a2b + 3ab2 - b3
f2(x) = ((2x)3 - 3(2x)2 + 3(2x) - 1) - (4x+6)(x2- 8x + 16) - (4x+12)(x2 - 2x + 1)
= (8x3 - 12x2 + 6x - 1) - (4x3-32x2+64x + 6x2 - 48x + 96) - (4x3 - 8x2 + 4x + 12x2 - 24x + 12)
= 8x3 - 12x2 + 6x - 1 - 4x3 + 262 - 16x - 96 - 4x3 - 4x2 + 20x - 12
= 10x2 + 10x - 85
polynôme du second degré
f3(x) = (2x3 + 2x - 1) (4x4 + 5x2 + 3) = 8x7 + 10x5 + 6x3 + 8x5 + 10x3 + 6x - 4x4 - 5x2 - 3
= 8x7 + 18x5 - 4x4 + 16x3 - 5x2 + 6x - 3
polynôme de degré 7
 = ax^3 + bx^2 + cx + d)
 = \dfrac{-3}{4}\quad \Leftrightarrow \quad a + b + c + d = \dfrac{-3}{4}\quad\quad\quad -) équation (1)
équation (1)
 = 1 \quad\Leftrightarrow \quad8a + 4b + 2c + d = 1 \quad\quad\quad -) équation (2)
équation (2)
 = \dfrac{-29}{4} \quad\Leftrightarrow \quad 27a + 9b + 3c + d = \dfrac{-29}{4}\quad\quad -) équation (3)
équation (3)
 = 21 \quad\Leftrightarrow \quad 64a + 16b + 4c + d = 21\quad\quad\quad -) équation (4)
équation (4)
on peut résoudre par substitution le système formé par ces 4 équations.
équation (1)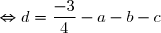
équations (1) et (2)
\quad \text{ donne } \quad d = \dfrac{-10}{4} + 6a + 2b)
équations (1),(2)et(3) + (\dfrac{-10}{4} + 6a + 2b) = \dfrac{-29}{4})

\quad \Rightarrow \quad c = -5 + 11a\quad et \quad (1)\quad \Rightarrow \quad d = 2 - 6a)
équations (1), (2), (3) et(4) + 4(-5 + 11a) + 2 - 6a = 21)

Reste à vérifier que les valeurs trouvées sont bien solutions du système proposé.

 = \dfrac{1}{2}x^3 - \dfrac{3}{4}x^2 + \dfrac{1}{2}x - 1 ) Publié par malou/carita
le
Publié par malou/carita
le
Polynômes : opérations sur les degrés
(exercices relatifs à cette fiche de cours)
exercice 1
Soit m un nombre réel donné. On considère la fonction polynôme définie par:Determiner le degré de P selon les valeurs de m.
exercice 2
On donne les fonctions polynômes :Exprimer
exercice 3
Déterminer le degré et les coefficients des fonctions polynômes suivantes, après les avoir écrites sous forme réduite et ordonnée :f1: x
f2: x
f3: x
exercice 4
Déterminer le polynôme P(x) de degré 3 tel que :P(1) =
exercice 1
Le polynôme est de degré 1
Le polynôme est de degré 2
Le polynôme est de degré 3
EXERCICE 2
f(x) = 2x3 - 5x + 1
g(x) = 3x4 - 2x2 + 7x - 3
(f+g)(x) = 3x4 + 2x3 - 2x2 + 2x -2
(fog)(x) = f(g(x)) = 2(3x4 - 2x2 + 7x - 3)3 - 5(3x4 - 2x2 + 7x - 3) + 1
détails du développement de (3x4 - 2x2 + 7x - 3)3
rappel (a+b)3 = a3 + 3a2b + 3ab2 + b3
on peut poser a = 3x4 - 2x2 = x2(3x2 - 2) et b = 7x - 3, ainsi :
(3x4 - 2x2 + 7x - 3)3 = (3x4 - 2x2)3 + 3(3x4 - 2x2)2(7x - 3) + 3(3x4 - 2x2)(7x - 3)2 + (7x - 3)3
détails du développement de (3x4 - 2x2)3
rappel (a-b)3 = a3 - 3a2b + 3ab2 - b3
détails du développement de 3(3x4 - 2x2)2(7x - 3)
détails du développement de 3(3x4 - 2x2)(7x - 3)2
détails du développement de (7x-3)3
on récapitule le développement de (3x4 - 2x2 + 7x - 3)3
on récapitule le développement de(fog)(x) = f(g(x))
(2f-3g)(x) = 2f(x) - 3g(x) = 2(2x3 - 5x + 1) - 3(3x4 - 2x3 + 7x - 3) = -9 x4 + 10x3 - 31x + 11
f2(x) = (fof)(x) = f(f(x)) = 2(2x3 - 5x + 1)3 - 5(2x3 - 5x + 1) + 1
détails du développement de 2(2x3 - 5x + 1)3
d'où
EXERCICE 3
f1(x) = (x - 1)2 - 4(2x - 3)(x + 2)2 + 3(x - 4)(x + 2) = x² - 2x + 1 - (8x - 12)(x2 + 4x + 4) + (3x - 12)(x + 2)= x² - 2x + 1 -(8x3 + 32x2 + 32x - 12x2 - 48x - 48)+ (3x2 + 6x - 12x - 24)
= - 8x3 - 16x2 + 8x + 25
polynôme de degré 3
f2(x) = (2x - 1)3 - 2(2x + 3)(x - 4)2 - 4(x - 1)2(x + 3)
rappel : (a-b)3 = a3 - 3a2b + 3ab2 - b3
f2(x) = ((2x)3 - 3(2x)2 + 3(2x) - 1) - (4x+6)(x2- 8x + 16) - (4x+12)(x2 - 2x + 1)
= (8x3 - 12x2 + 6x - 1) - (4x3-32x2+64x + 6x2 - 48x + 96) - (4x3 - 8x2 + 4x + 12x2 - 24x + 12)
= 8x3 - 12x2 + 6x - 1 - 4x3 + 262 - 16x - 96 - 4x3 - 4x2 + 20x - 12
= 10x2 + 10x - 85
polynôme du second degré
f3(x) = (2x3 + 2x - 1) (4x4 + 5x2 + 3) = 8x7 + 10x5 + 6x3 + 8x5 + 10x3 + 6x - 4x4 - 5x2 - 3
= 8x7 + 18x5 - 4x4 + 16x3 - 5x2 + 6x - 3
polynôme de degré 7
EXERCICE 4
Soiton peut résoudre par substitution le système formé par ces 4 équations.
équation (1)
équations (1) et (2)
équations (1),(2)et(3)
équations (1), (2), (3) et(4)
Reste à vérifier que les valeurs trouvées sont bien solutions du système proposé.
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir l'énoncé seul
Voir l'énoncé seul forum de première
forum de première